Some years ago, I wrote code in Sage to solve the Quantumino puzzle. I also used it to make a one-minute video illustrating the Dancing links algorithm which I am proud to say it is now part of the Dancing links wikipedia page.

I must say that the video is not perfect. On wikipedia, the file talk page of the video says that the Jerky camera movement is distracting. That is because I managed to make the video out of images created by .show(viewer='tachyon') which changes the coordinate system, hardcodes a lot of parameters, zoom properly, simplifies stuff to make sure the user don't see just a blank image. But, for making a movie, we need access to more parameters especially the placement of the camera (to avoid the jerky movement). I know that Tachyon allows all of that. It is still a project that I have to create a more versatile Graphics3D -> Tachyon conversion allowing to construct nice videos of evolving mathematical objects. That's another story.
Let me recall that the goal of the Quantumino puzzle is to fill a \(2\times 5\times 8\) box with 16 out of 17 three-dimensional pentaminos. After writing the sage code to solve the puzzle, one question was left: how many solutions are there? Is the official website realist or very prudent when they say that there are over 10.000 potential solutions? Can it be computed in hours? days? months? years? ... or light-years!? The only thing I knew was that the following computation (letting the 0-th pentamino aside) never finished on my machine:
sage:fromsage.games.quantuminoimportQuantuminoSolversage:QuantuminoSolver(0).number_of_solutions()
Since I spent already too much time on this side-project, I decided in 2012 to stop spending any more time on it and to really focus on finishing writing my thesis.
So before I finish writing my thesis, I knew that the computation was not going to take a light-year, since I was able to finish the computation of the number of solutions when the 0-th pentamino is put aside and when the 1-st pentamino is pre-positioned somewhere in the box. That computation completed in 4 hours on my old laptop and gave about 5 millions solutions. There are 17 choices of pentatminos to put aside, there are 360 distinct positions of the 1-st pentamino, so I estimated the number of solution to be something like \(17\times 360\times 5000000 = 30 \times 10^9\). Most importantly, I estimated the computation to take \(17\times 360\times 4= 24480\) hours or 1020 days. Therefore, I knew I could not do it on my laptop.
But last year, I received an email from the designer of the Quantumino puzzle:
-------- Message transféré -------- Sujet : quantumino Date : Tue, 09 Dec 2014 13:22:30 +0100 De : Nicolaas Neuwahl Pour : Sebastien Labbe hi sébastien labbé, i'm the designer of the quantumino puzzle. i'm not a mathematician, i'm an architect. i like mathematics. i'm quite impressed to see the sage work on quantumino, also i have not the knowledge for full understanding. i have a question for you - can you tell me HOW MANY different quantumino- solutions exist? ty and bye nicolaas neuwahl
This summer was a good timing to launch the computation on my beautiful Intel® Core™ i5-4590 CPU @ 3.30GHz × 4 at Université de Liège. First, I improved the Sage code to allow a parallel computation of number of solutions in the dancing links code (#18987, merged in a Sage 6.9.beta6). Secondly, we may remark that each tiling of the \(2\times 5\times 8\) box can be rotated in order to find 3 other solutions. It is possible to gain a factor 4 by avoiding to count 4 times the same solution up to rotations (#19107, still needs work from myself). Thanks to Vincent Delecroix for doing the review on both ticket.
With those two tickets (some previous version to be honest) on top of sage-6.8, I started the computation on August 4th and the computation finished last week on September 18th for a total of 45 days. The computation was stopped only once on September 8th (I forgot to close firefox and thunderbird that night...).
The number of solutions and computation time for each pentamino put aside together with the first solution found is shown in the table below. We remark that some values are equal when the aside pentaminoes are miror images (why!?:).
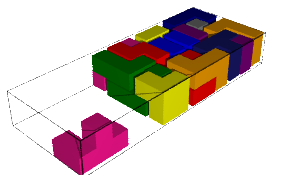 | 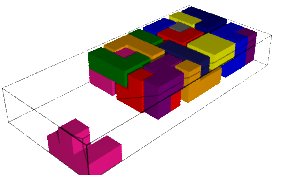 |
| 634900493 solutions | 634900493 solutions |
| 2 days, 6:22:44.883358 | 2 days, 6:19:08.945691 |
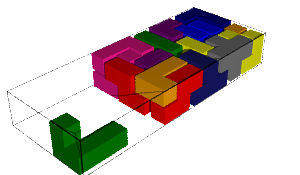 | 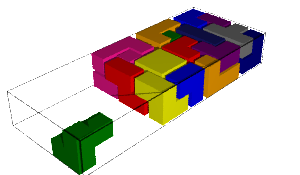 |
| 509560697 solutions | 509560697 solutions |
| 2 days, 0:01:36.844612 | 2 days, 0:41:59.447773 |
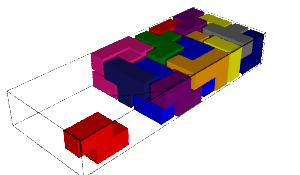 | 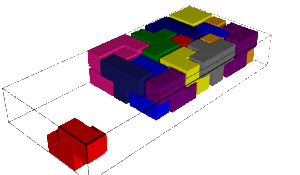 |
| 628384422 solutions | 628384422 solutions |
| 2 days, 7:52:31.459247 | 2 days, 8:44:49.465672 |
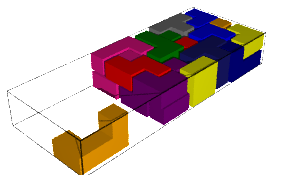 | 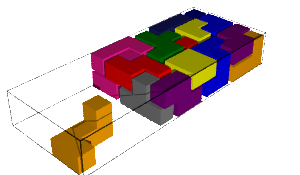 |
| 1212362145 solutions | 1212362145 solutions |
| 3 days, 17:25:00.346627 | 3 days, 19:10:02.353063 |
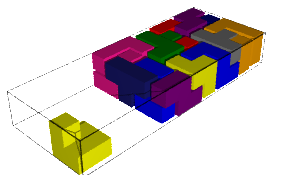 | 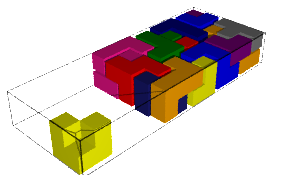 |
| 197325298 solutions | 556534800 solutions |
| 22:51:54.439932 | 1 day, 19:05:23.908326 |
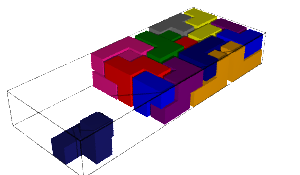 | 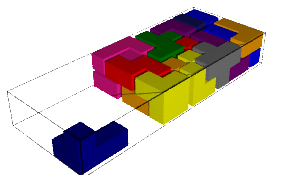 |
| 664820756 solutions | 468206736 solutions |
| 2 days, 8:48:54.767662 | 1 day, 20:14:56.014557 |
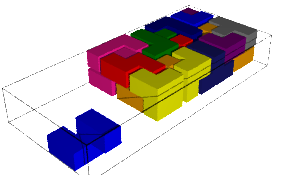 | 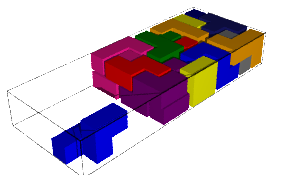 |
| 1385955043 solutions | 1385955043 solutions |
| 4 days, 1:40:30.270929 | 4 days, 4:44:05.399367 |
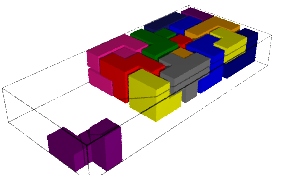 | 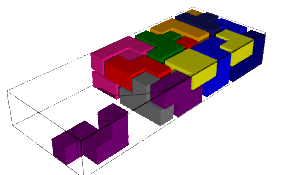 |
| 694998374 solutions | 694998374 solutions |
| 2 days, 11:44:29.631 | 2 days, 6:01:57.946708 |
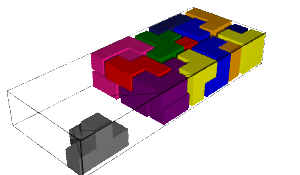 | |
| 1347221708 solutions | |
| 3 days, 21:51:29.043459 |
Therefore the total number of solutions up to rotations is \(13 366 431 646 \approx 13\times 10^9\) which is indeed more than 10000:)
sage:L=[634900493,634900493,509560697,509560697,628384422,628384422,1212362145,1212362145,197325298,556534800,664820756,468206736,1385955043,1385955043,694998374,694998374,1347221708]sage:sum(L)13366431646sage:factor(_)2*23*271*1072231
| The machine (4 cores) | Intel® Core™ i5-4590 CPU @ 3.30GHz × 4 (Université de Liège) |
| Computation Time | 45 days, (Aug 4th -- Sep 18th, 2015) |
| Number of solutions (up to rotations) | 13.366.431.646 |
| Number of solutions / cpu / s | 859.47 |
My code will be available on github.