We are the SageMathCloud developers!
This is just a test and we love math:
$\Phi(x) = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^x e^{-\xi^2/2}\; d\xi$
Expect more soon!
↧
SageMathCloud: Hello World
↧
SageMathCloud: Creating Custom “Mode Commands” in Sage Worksheets
What is a Mode Command?
By default, running a cell in a Sage worksheet causes the input to be run as Sage commands, with output from Sage written to the output of the cell. Mode commands in a Sage worksheet cause the input to be run through some other process to create cell output. For example,
- Typing
%mdat the start of a cell causes cell input to be rendered as markdown in the cell output. - Typing
%rcauses cell input to be treated as statements in the R language, with corresponding output. - Typing
%HTMLcauses cell input to be treated as HTML, rendered as the output.
There are many built-in modes (e.g. Cython, GAP, Pari, R, Python, Markdown, HTML, etc…)
Note: If it is not the default mode of your *.sagews worksheet, a mode command must be the first line of a cell. In other words, make sure the command %md, %r, or %HTML is the first line of a cell.
Alternatively, you can make any mode the default for all cells in the worksheet using %default_mode <some_mode>. Then all cells will be using that chosen mode. If you choose this approach, you may still explicitly use %sage for cells you want processed by the Sage interpreter (or %foo to explicitly switch to any non-default mode).
There is an entire section of the FAQ page SageMathCloud Worksheet (and User Interface) Help dedicated to questions about the built-in modes. It had 10 questions-and-answers in it as of July 28, 2016.
Is there a list of all currently supported % modes in SageMathCloud?
You can view available built-in modes by selecting Help > Mode commands in the Sage toolbar while cursor is in a sage cell. That will
insert the line print('\n'.join(modes())) into the current cell.
What is a Custom Mode Command?
Custom mode commands are modes defined by the user. Like any mode command, a custom mode command processes the input section of a cell and writes the output. As stated in the help for modes,
Create your own mode command by defining a function that takes a string as input and outputs a string. (Yes, it is that simple.)
Examples of Custom Mode Commands
Custom mode commands can be used to - render or compile cell input into cell output - send commands to other processes and show the results
Here are some examples:
Example 1: View CSV data as a table
Define the mode in a sage cell, as follows:
importpandasaspdfromStringIOimportStringIOdefcsv_table(str):print(pd.read_csv(StringIO((str)),index_col=0))Input:
%csv_table
Sample,start,middle,end
A,2,5,51
B,6,8,11
C,7,22,41Output:
start middle end
Sample
A 2 5 51
B 6 8 11
C 7 22 41NOTE: Sage’s show command is also aware of Pandas tables,
so if you instead define
defcsv_table(str):show(pd.read_csv(StringIO((str)),index_col=0))then %csv_table will produce nice HTML output.
Example 2: View JSON converted to YAML
Define the mode:
importjsonimportyamldefj2y(str):print(yaml.safe_dump(json.loads(str)))Input:
%j2y{"foo":"bar","baz":["xyzzy","plugh"]}Output:
baz:[xyzzy,plugh]foo:barExample 3: Convert Units of Measure
In this example, each input line is a number with units, possibly followed by target units. If target units are not specified, SI units are the target. This example uses the Sage Units of Measurement package.
Define the mode:
defconvert_units(str):forlineinstr.split('\n'):if'units'inline:lval=eval(line)ifisinstance(lval,tuple):print(lval[0].convert(lval[1]))else:print(lval.convert())Input:
%convert_units# pounds to kilograms175.0*units.mass.pound# miles to kilometers3.0*units.length.mile,units.length.kilometer# an adult doing moderate exercise might burn 200 kcal per hour# convert to watts200.0*units.energy.calorie*units.si_prefixes.kilo/units.time.hour,units.power.wattOutput:
79.37866475*kilogram4.828032*kilometer232.6*wattExample 4: Display Reverse Complement of Nucleotide Sequences
This example uses Biopython, which is already installed on SageMathCloud.
Define the mode:
fromBio.SeqimportSeqdefrevcomp(str):s=Seq(str)print(s.reverse_complement())Input:
%revcompATGCGCTCCGACACTTTOutput:
AAAGTGTCGGAGCGCATExample 5: Run Multiple Shell Processes
Suppose you want several bash processes with different working directories or environment variables controlled from the same worksheet. You can use the built-in jupyter command to create several custom modes.
More information on “the sage-jupyter bridge” is available at Sage Jupyter. Code creating a mode for anaconda3 is available by selecting Modes > Jupyter bridge. You can view available Jupyter kernels by selecting Help > Jupyter kernels in the Sage toolbar while cursor is in a sage cell. That will
insert the line print(jupyter.available_kernels()) into the current cell.
Define the modes:
sh1=jupyter("bash")sh2=jupyter("bash")Cell 1:
%sh1# show PID of current sh processecho$BASHPID--output--23723Cell 2:
%sh2echo$BASHPID--output--23727Cell 3:
%sh1echo$BASHPID--output--23723Example 6: Connect to Remote Server and Run Shell Commands
In this example, any cell in the custom mode consists of shell commands to be run on a remote server. The same session is used for all cells in the given mode.
Notes: - The SageMathCloud project must have Internet access. This is an upgrade, only available to users with a paid subscription. (See also “Why Should I Purchase a Subscription?”.) - Configure ssh public and private keys with empty passphrase. - Set host and user for the remote connection. - You may want to set IdentityFile in your ~/.ssh/config file.
Define the mode:
%sagefrompexpectimportpxsshfromansi2htmlimportAnsi2HTMLConverterconv=Ansi2HTMLConverter(inline=True,linkify=True)s=pxssh.pxssh(echo=False)host='myhost.mydomain.org'user='joe'ifs.login(host,user):defsshexec(code):forlineincode.split('\n'):s.sendline(line)s.prompt()h=s.beforeh=conv.convert(h,full=False)h='<pre style="font-family:monospace;">'+h+'\n</pre>'salvus.html(h)print'sshexec defined; logout with s.logout()'else:print'sshexec setup failed'Input:
%sshexeclscd/tmpOutput:
...lslisting,showingcolor-lsoutputifavailable...Input in second cell, showing that working directory is retained
%sshexecpwdExample 7: Nicely typesetting output from the FriCAS computer algebra system
The following function takes whatever the cell input is, executes the code in FriCAS, performs some simple substitutions on the FriCAS output and then displays it using Markdown:
Define the mode:
%sagedeffricas_tex(s):importret=fricas.eval(s)t=re.compile(r'\r').sub('',t)# mathml overbart=re.compile(r'¯').sub('‾',t,count=0)# cleanup FriCAS LaTeXt=re.compile(r'\\leqno\(.*\)\n').sub('',t)t=re.compile(r'\\sb ').sub('_',t,count=0)t=re.compile(r'\\sp ').sub('^',t,count=0)md(t,hide=False)With this mode, FriCAS can generate output that is (almost) compatible with Markdown format.
For example you can use this new mode in a cell with the following input:
%fricas_tex)setoutputalgebraoff)setoutputmathmlon)setoutputtexonsqrt(2)/2+1Output: This will evaluate ‘sqrt(2)/2+1’ and display the result in both LaTeX format and MathML formats (in a MathML capable browser).
Note: The current version of Sage (6.6 and earlier) requires a patch to correct a bug in the fricas/axiom interface.
↧
↧
SageMathCloud: How do I start a Jupyter kernel in a SageMath Worksheet?
For a quick reminder, sample code is available for opening an Anaconda3 session. In the Sage worksheet toolbar, select Modes > Jupyter bridge.
Use the jupyter command to launch any installed Jupyter kernel from a Sage worksheet
py3=jupyter("python3")After that, any cell that begins with %py3 will send statements to the Python3 kernel that you just started. If you want to draw graphics, there is no need to call %matplotlib inline.
%py3print(42)importnumpyasnp;importpylabaspltx=np.linspace(0,3*np.pi,500)plt.plot(x,np.sin(x**2))plt.show()You can set the default mode to be your Jupyter kernel for all cells in the worksheet: after putting the following in a cell, click the “restart” button, and you have an anaconda worksheet.
%autoanaconda3=jupyter('anaconda3')%default_modeanaconda3Each call to jupyter() launches its own Jupyter kernel, so you can have more than one instance of the same kernel type in the same worksheet session.
p1=jupyter('python3')p2=jupyter('python3')p1('a = 5')p2('a = 10')p1('print(a)')# prints 5p2('print(a)')# prints 10↧
Lauren Devitt: Final GSOC Report
Over the summer I have been coding for SAGE as part of Google Summer of Code 2016. I feel this opportunity has strengthened both my skills as a coder and as a mathematician. SAGE is an open source math software system, used to do calculations. SAGE is made up of code available for free public use and modification. It is a collaborative effort where people from around the world can add new code, update old code, and share the changes that they make. Open source coding is a labor of
↧
Extending Matroid Functionality Google Summer of Code 2016: Overview of what was done
My project has been extending the functionality of SageMath in a matroid direction.
As part of my application, and before the summer officially started, I worked on two tickets: https://trac.sagemath.org/ticket/20290 and https://trac.sagemath.org/ticket/14666. The first was fixing a typo (and learning how to use the interface), and the second one modified the code to find a maximum weighted basis of a matroid so that a user could also see if there was exactly one maximum weighted basis. These are both currently incorporated into official release version of SageMath.
At the beginning of the summer, I was focused on adding certificates to the pre written algorithms is_isomorphic(), chordal functions, has_minor(), and has_line_minor(). All of these are closed tickets except the last one, which had a merge conflict. This also enabled me to get a feel for the documentation culture of my organization.
The bulk of my project has been working on implementing An Almost Linear-Time Algorithm for Graph Realization by Robert Bixby and Donald Wagner. This algorithm was written with data structures that didn't exactly match the code base that I was incorporating the function into, so some changes were made there, and some simple (but not necessarily easy) supporting functions were added. There are still some bugs in the code, whose current version can be found here. Much of the rest of this post will be devoted to explaining the data structures that we used for the algorithm. It is aimed mostly at whoever (hopefully future me) is going to finish this function.
We used two new data structures Node, and Decomposition. The decomposition is composed of nodes and relations between them. In particular, it contains a directed tree, where each vertex corresponds to a node. A decomposition also stores information which is useful to the functions that need it. The root of the tree is stored, as are the nodes which contain the first and last verticies of the hypopath along with these verticies. Also stored are integers to makes sure that we don't double name two verticies or two edges the same thing.
A node contains a graph, a parent marker edge, and a parent marker vertex. The latter is one of the vertices of the parent marker edge, and is manipulated so that it is the edge which will end up being included in the path that comes from the hypopath. It also stores an integer T, which depends on the iteration of adding edges, and is stored after being computed.
The flow structure of the main functions is given below. Each function is a decomposition function.
![]()
As part of my application, and before the summer officially started, I worked on two tickets: https://trac.sagemath.org/ticket/20290 and https://trac.sagemath.org/ticket/14666. The first was fixing a typo (and learning how to use the interface), and the second one modified the code to find a maximum weighted basis of a matroid so that a user could also see if there was exactly one maximum weighted basis. These are both currently incorporated into official release version of SageMath.
At the beginning of the summer, I was focused on adding certificates to the pre written algorithms is_isomorphic(), chordal functions, has_minor(), and has_line_minor(). All of these are closed tickets except the last one, which had a merge conflict. This also enabled me to get a feel for the documentation culture of my organization.
The bulk of my project has been working on implementing An Almost Linear-Time Algorithm for Graph Realization by Robert Bixby and Donald Wagner. This algorithm was written with data structures that didn't exactly match the code base that I was incorporating the function into, so some changes were made there, and some simple (but not necessarily easy) supporting functions were added. There are still some bugs in the code, whose current version can be found here. Much of the rest of this post will be devoted to explaining the data structures that we used for the algorithm. It is aimed mostly at whoever (hopefully future me) is going to finish this function.
We used two new data structures Node, and Decomposition. The decomposition is composed of nodes and relations between them. In particular, it contains a directed tree, where each vertex corresponds to a node. A decomposition also stores information which is useful to the functions that need it. The root of the tree is stored, as are the nodes which contain the first and last verticies of the hypopath along with these verticies. Also stored are integers to makes sure that we don't double name two verticies or two edges the same thing.
A node contains a graph, a parent marker edge, and a parent marker vertex. The latter is one of the vertices of the parent marker edge, and is manipulated so that it is the edge which will end up being included in the path that comes from the hypopath. It also stores an integer T, which depends on the iteration of adding edges, and is stored after being computed.
The flow structure of the main functions is given below. Each function is a decomposition function.
Here is the list of all the functions and the status of each of them. Most of them are supporting functions, with the exception of relink1, typing, relink2, and hypopath from section 4 of the paper, squeeze and update from section 5, and is_graphic from section 6.
Nodes
get_graph(self)
Done
get_parent_marker(self)
Done
get_named_edge(self, f)
Done
get_parent_marker_edge(self)
Done
get_f(self)
Done
set_f(self, int n)
Done
is_polygon(self)
Done
s_path(self, P)
Done
is_cycle(self, P)
Done
_T(self, P, Z=*)
This will correctly give the T value when self is a leaf of the reduced arborescence. It does not correctly compute the T value otherwise.
__relink1(self, Z=*, WQ=*)
Done
__relink2(self, Z=*, WQ=*)
Done
get_T(self)
Done
set_T(self, int T)
Done
CunninghamEdmondsDecomposition
relink1(self, Q, Z=*, WQ=*)
Done
get_D_hat(self, P)
Done
T(self, N, P, T)
This is not done. It needs to be fixed so that it takes into account the types of the children of self.
__typing(self, P, pi)
This is not tested as it relies on T. There are, however, no known deficiencies with the algorithm.
__relink2(Q, Z=*, WQ=*)
Done
__hypopath(self, P)
This is not tested as it relies on __typing. The assigning of u_1 and u_2 needs to be fixed.
__squeeze(self, N, L)
Done
__update(self, P, C)
This is not tested as it relies on __hypopath. It is essentially done, except that the variables u_1, u_2, K_1, and K_2 are not necessarily computed correctly, and U2.4 is not written.
__is_graphic(self)
This is not done. G2 and G3 need to be written, and it needs to be tested. This cannot happen until the rest of the problems are fixed.
merge_with_parent(self, N, N_vertex=*, P_vertex=*)
This is done, but it doesn't use the f is N_vertex and P_vertex are undefined. This should probably be changed.
merge_branch(self, N, P)
This is written, but in order to insure that the intersection of P with this graph is always a path if possible, P should be replaced with P_0, and the parent markers of children that intersect P should be added to P_0 initially, and removed, in turn, when that child is merged with N.
__add_cycle(self, cycle)
Done
get_arborescence(self)
Done
get_nodes(self)
Done
get_root(self)
Done
__get_pi(self)
This is done, but it should be changed so that it can take a sub tree of self.arborescence as an input, and give pi on the reduced decomposition.
branch(self, N)
Done
get_parent(self, N)
Done
↧
↧
SageMathCloud: First Status Update
William scripted status reports, organized several things related to billing, and spent hours working on subtle issues related to sync and file saving. Harald worked on the SMC blog, read emails, and triaged tickets. Hal continued experiments with pytest for smc_sagews, resumed work on sagews issues (note PR823 is ready for review), updated MOOC companion for complex variables, and explored supporting .Rmd files and %Rmd sagews mode. Tim made three pull requests for realtime list of collaborators viewing any file in a project, restoring tabs, and make deletion immediately delete files from disk instead of moving them to the trash, since we have snapshots.
↧
SageMathCloud: First Nightly Changelog
Our Nightly Changelog keeps you updated on small feature changes, bugfixes, and quality of life improvements. For upcoming changes, see our weekly progress report column.
General Usage
- Deleting a file now deletes it instead of moving it to the trash. To retrieve deleted files, use snapshots.
Quality of Life
- Improved file saving and syncing
↧
William Stein
Funding Open Source Mathematical Software in the United States
I do not know how to get funding for open source mathematical software in the United States. However, I'm trying.Why: Because Sage is Hobbling Along
Despite what we might think in our Sage-developer bubble, Sage is hobbling along, and without an infusion of financial support very soon, I think the project is going to fail in the next few years. I have access to Google analytics data for sagemath.org since 2007, and there has been no growth in active users of the website since 2011:
Something that is Missing
The worse part of all for me, after ten years, is seeing things like this email today from John Palmieri, where he talks about writing slow but interesting algebraic topology code, and needing help from somebody who knows Cython to actually make his code fast.I know from my three visits to the Magma group in Sydney that such assistance is precisely what having real financial support can provide. Such money makes it possible to have fulltime people who know the tools and how to optimize them well, and they work on this sort of speedup and integration -- this "devil is in the details" work -- for each major contribution (they are sort of like a highly skilled version of a journal copy editor and referee all in one). Doing this makes a massive difference, but also costs on the order of $1 million / year to have any real impact. 1 million is probably the Magma budget to support around 10 people and periodic visitors, and of course like 1% of the budget of Matlab/Mathematica. Magma has this support partly because Magma is closed source, and maintains tight control on who may use it.
Searching for a Funding Model
Sage is open source and freely available to all, so it is of potential huge value to the community by being owned by everybody and changeable. However, those who fund Magma (either directly or indirectly) haven't funded Sage at the same level for some reason. I can't make Sage closed source and copy that very successful funding model. I've tried everything I can think of given the time and resources I have, and the only model left that seems able to support open source is having a company that does something else well and makes money, then using some of the profit to fund open source (Intel is the biggest contributor to Linux).SageMath, Inc.
Since I failed to find any companies that passionately care about Sage like Intel/Google/RedHat/etc. care about Linux, I started one. I've been working on SageMathCloud extremely hard for over 3 years now, with the hopes that at least it could be a way to fund Sage development.↧
William Stein: SageMath: "it's not research"
The University of Washington (UW) mathematics department has funding for grad students to "travel to conferences". What sort of travel funding?
One of my two Ph.D. students at UW asked our Grad program director: "I'll be going to Joint Mathematics Meetings (JMM) to help out at the SageMath booth. Is this a thing I can get funding for?"
ANSWER: Travel funds are primarily meant to support research, so although I appreciate people helping out at the SageMath booth, I think that's not the best use of the department's money.
I think this "it's not research" perspective on the value of mathematical software is unfortunate and shortsighted. Moreover, it's especially surprising as the person who wrote the above answer has contributed substantially to the algebraic topology functionality of Sage itself, so he knows exactly what Sage is.
Sigh. Can some blessed person with an NSF grant out there pay for this grad student's travel expenses to help with the Sage booth? Or do I have to use the handful of $10, $50, etc., donations I've got the last few months for this purpose?
- The department has some money available.
- The UW Graduate school has some money available: They only provide funding for students giving a talk or presenting a poster.
- The UW GPSS has some money available: contact them directly to apply (they only provide funds for "active conference participation", which I think means giving a talk, presenting a poster, or similar)
One of my two Ph.D. students at UW asked our Grad program director: "I'll be going to Joint Mathematics Meetings (JMM) to help out at the SageMath booth. Is this a thing I can get funding for?"
ANSWER: Travel funds are primarily meant to support research, so although I appreciate people helping out at the SageMath booth, I think that's not the best use of the department's money.
I think this "it's not research" perspective on the value of mathematical software is unfortunate and shortsighted. Moreover, it's especially surprising as the person who wrote the above answer has contributed substantially to the algebraic topology functionality of Sage itself, so he knows exactly what Sage is.
Sigh. Can some blessed person with an NSF grant out there pay for this grad student's travel expenses to help with the Sage booth? Or do I have to use the handful of $10, $50, etc., donations I've got the last few months for this purpose?
↧
↧
William Stein: RethinkDB must relicense NOW
What is RethinkDB?
RethinkDB is a INCREDIBLE high quality polished open source realtime database that is easy to deploy, shard, replicate, and supports a reactive client programming model, which is useful for collaborative web-based applications. Shockingly, the 7-year old company that created RethinkDB has just shutdown. I am the CEO of a company, SageMath, Inc., that uses RethinkDB very heavily, so I have a strong interest in RethinkDB surviving as an independent open source project.Three Types of Open Source Projects
There are many types of open source projects. RethinkDB was the type of open source project where most work on RethinkDB has been fulltime focused work, done by employees of the RethinkDB company. RethinkDB is licensed under the AGPL, but the company promised to make the software available to customers under other licenses.Academia: I started the SageMath open source math software project in 2005, which has over 500 contributors, and a relatively healthy volunteer ecosystem, with about hundred contributors to each release, and many releases each year. These are mostly volunteer contributions by academics: usually grad students, postdocs, and math professors. They contribute because SageMath is directly relevant to their research, and they often contribute state of the art code that implements algorithms they have created or refined as part of their research. Sage is licensed under the GPL, and that license has worked extremely well for us. Academics sometimes even get significant grants from the NSF or the EU to support Sage development.
Companies: I also started the Cython compiler project in 2007, which has had dozens of contributors and is now the defacto standard for writing or wrapping fast code for use by Python. The developers of Cython mostly work at companies (e.g., Google) as a side project in their spare time. (Here's a message today about a new release from a Cython developer, who works at Google.) Cython is licensed under the Apache License.
What RethinkDB Will Become
RethinkDB will no longer be an open source project whose development is sponsored by a single company dedicated to the project. Will it be an academic project, a company-supported project, or dead?A friend of mine at Oxford University surveyed his academic CS colleagues about RethinkDB, and they said they had zero interest in it. Indeed, from an academic research point of view, I agree that there is nothing interesting about RethinkDB. I myself am a college professor, and understand these people! Academic volunteer open source contributors are definitely not going to come to RethinkDB's rescue. The value in RethinkDB is not in the innovative new algorithms or ideas, but in the high quality carefully debugged implementations of standard algorithms (largely the work of bad ass German programmer Daniel Mewes). The RethinkDB devs had to carefully tune each parameter in those algorithms based on extensive automated testing, user feedback, the Jepsen tests, etc.
That leaves companies. Whether or not you like or agree with this, many companies will not touch AGPL licensed code:
"Google open source guru Chris DiBona says that the web giant continues to ban the lightning-rod AGPL open source license within the company because doing so "saves engineering time" and because most AGPL projects are of no use to the company."This is just the way it is -- it's psychology and culture, so deal with it. In contrast, companies very frequently embrace open source code that is licensed under the Apache or BSD licenses, and they keep such projects alive. The extremely popular PostgreSQL database is licensed under an almost-BSD license. MySQL is freely licensed under the GPL, but there are good reasons why people buy a commercial MySQL license (from Oracle) for MySQL. Like RethinkDB, MongoDB is AGPL licensed, but they are happy to sell a different license to companies.
With RethinkDB today, the only option is AGPL. This very strongly discourage use by the only possible group of users and developers that have any chance to keep RethinkDB from death. If this situation is not resolved as soon as possible, I am extremely afraid that it never will be resolved. Ever. If you care about RethinkDB, you should be afraid too. Ignoring the landscape and culture of volunteer open source projects is dangerous.
A Proposal
I don't know who can make the decision to relicense RethinkDB. I don't kow what is going on with investors or who is in control. I am an outsider. Here is a proposal that might provide a way out today:PROPOSAL: Dear RethinkDB, sell me an Apache (or BSD) license to the RethinkDB source code. Make this the last thing your company sells before it shuts down. Just do it.
Hacker News Discussion
↧
Lauren Devitt: Knots by Number, Quipu
For my undergraduate thesis my focus was in knot theory, a subset of topology and a newer subject in mathematics. These are not the knots we think of in our daily life. The knots I studied had no ends and no thickness. Knots as we know them in everyday life have been around since before the Greeks. The book of Kells is decorated with intricate knot work. Sailors have used them on their ships. The Incas even used them to keep track of their accounting.
The Incan civilization started in modern day
↧
William Stein: RethinkDB, SageMath, Andreessen-Horowitz, Basecamp and Open Source Software
RethinkDB and sustainable business models
Three weeks ago, I spent the evening of Sept 12, 2016 with Daniel Mewes, who is the lead engineer of RethinkDB (an open source database). I was also supposed to meet with the co-founders, Slava and Michael, but they were too busy fundraising and couldn't join us. I pestered Daniel the whole evening about what RethinkDB's business model actually was. Yesterday, on October 6, 2016, RethinkDB shut down.I met with some RethinkDB devs because an investor who runs a fund at the VC firm Andreessen-Horowitz (A16Z) had kindly invited me there to explain my commercialization plans for SageMath, Inc., and RethinkDB is one of the companies that A16Z has invested in. At first, I wasn't going to take the meeting with A16Z, since I have never met with Venture Capitalists before, and do not intend to raise VC. However, some of my advisors convinced me that VC's can be very helpful even if you never intend to take their investment, so I accepted the meeting.
In the first draft of my slides for my presentation to A16Z, I had a slide with the question: "Why do you fund open source companies like RethinkDB and CoreOS, which have no clear (to me) business model? Is it out of some sense of charity to support the open source software ecosystem?" After talking with people at Google and the RethinkDB devs, I removed that slide, since charity is clearly not the answer (I don't know if there is a better answer than "by accident").
I have used RethinkDB intensely for nearly two years, and I might be their biggest user in some sense. My product SageMathCloud, which provides web-based course management, Python, R, Latex, etc., uses RethinkDB for everything. For example, every single time you enter some text in a realtime synchronized document, a RethinkDB table gets an entry inserted in it. I have RethinkDB tables with nearly 100 million records. I gave a talk at a RethinkDB meetup, filed numerous bug reports, and have been described by them as "their most unlucky user". In short, in 2015 I bet big on RethinkDB, just like I bet big on Python back in 2004 when starting SageMath. And when visiting the RethinkDB devs in San Francisco (this year and also last year), I have said to them many times "I have a very strong vested interest in you guys not failing." My company SageMath, Inc. also pays RethinkDB for a support contract.
Sustainable business models were very much on my mind, because of my upcoming meeting at A16Z and the upcoming board meeting for my company. SageMath, Inc.'s business model involves making money from subscriptions to SageMathCloud (which is hosted on Google Cloud Platform); of course, there are tons of details about exactly how our business works, which we've been refining based on customer feedback. Though absolutely all of our software is open source, what we sell is convenience, easy of access and use, and we provide value by hosting hundreds of courses on shared infrastructure, so it is much cheaper and easier for universities to pay us rather than hosting our software themselves (which is also fairly easy). So that's our business model, and I would argue that it is working; at least our MRR is steadily increasing and is more than twice our hosting costs (we are not cash flow positive yet due to developer costs).
So far as I can determine, the business model of RethinkDB was to make money in the following ways: 1. Sell support contracts to companies (I bought one). 2. Sell a closed-source proprietary version of RethinkDB with extra features that were of interest to enterprise (they had a handful of such features, e.g., audit logs for queries). 3. Horizon would become a cloud-hosted competitor to Firebase, with unique advantages that users have the option to migrate from the cloud to their own private data center, and more customizability. This strategy depends on a trend for users to migrate away from the cloud, rather than to it, which some people at RethinkDB thought was a real trend (I disagree).
I don't know of anything else they were seriously trying right now. The closed-source proprietary version of RethinkDB also seemed like a very recent last ditch effort that had only just begun; perhaps it directly contradicted a desire to be a 100% open source company?
With enough users, it's easier to make certain business models work. I suspect RethinkDB does not have a lot of real users. Number of users tends to be roughly linearly related to mailing list traffic, and the RethinkDB mailing list has an order of magnitude less traffic compared to the SageMath mailing lists, and SageMath has around 50,000 users. RethinkDB wasn't even advertised to be production ready until just over a year ago, so even they were telling people not to use it seriously until relatively recently. The adoption cycle for database technology is slow -- people wisely wait for Aphyr's tests, benchmarks comparing with similar technology, etc. I was unusual in that I chose RethinkDB much earlier than most people would, since I love the design of RethinkDB so much. It's the first database I loved, having seen a lot over many decades.
Conclusion: RethinkDB wasn't a real business, and wouldn't become one without year(s) more runway.
I'm also very worried about the future of RethinkDB as an open source project. I don't know if the developers have experience growing an open source community of volunteers; it's incredibly hard and its unclear they are even going to be involved. At a bare minimum, I think they must switch to a very liberal license (Apache instead of AGPL), and make everything (e.g., automated testing code, documentation, etc) open source. It's insanely hard getting any support for open source infrastructure work -- support mostly comes from small government grants (for research software) or contributions from employees at companies (that use the software). Relicensing in a company friendly way is thus critical.
Company Incentives
Companies can be incentived in various ways, including:- to get to the next round of VC funding
- to be a sustainable profitable business by making more money from customers than they spend, or
- to grow to have a very large number of users and somehow pivot to making money later.
For me, SageMath is an open source project I started in 2004, and I'm in it for the long haul. I will make the business I'm building around SageMathCloud succeed, or I will die trying -- therefore I have very, very little tolerance for risk. Failure is not an option, and I am not looking for an exit. For me, the strategy that best matches my values is to incentive my company to build a profitable business, since that is most likely to survive, and also to give us the freedom to maintain our longterm support for open source and pure mathematics software.
Thus for my company, neither optimizing for raising the next round of VC or growing at all costs makes sense. You would be surprised how many people think I'm completely wrong for concluding this.
Andreessen-Horowitz
I spent the evening with RethinkDB developers, which scared the hell out of me regarding their business prospects. They are probably the most open source friendly VC-funded company I know of, and they had given me hope that it is possible to build a successful VC-funded tech startup around open source. I prepared for my meeting at A16Z, and deleted my slide about RethinkDB.I arrived at A16Z, and was greeted by incredibly friendly people. I was a little shocked when I saw their nuclear bomb art in the entry room, then went to a nice little office to wait. The meeting time arrived, and we went over my slides, and I explained my business model, goals, etc. They said there was no place for A16Z to invest directly in what I was planning to do, since I was very explicit that I'm not looking for an exit, and my plan about how big I wanted the company to grow in the next 5 years wasn't sufficiently ambitious. They were also worried about how small the total market cap of Mathematica and Matlab is (only a few hundred million?!). However, they generously and repeatedly offered to introduce me to more potential angel investors.
We argued about the value of outside investment to the company I am trying to build. I had hoped to get some insight or introductions related to their portfolio companies that are of interest to my company (e.g., Udacity, GitHub), but they deflected all such questions. There was also some confusion, since I showed them slides about what I'm doing, but was quite clear that I was not asking for money, which is not what they are used to. In any case, I greatly appreciated the meeting, and it really made me think. They were crystal clear that they believed I was completely wrong to not be trying to do everything possible to raise investor money.
Basecamp
During the first year of SageMath, Inc., I was planning to raise a round of VC, and was doing everything to prepare for that. I then read some of DHH's books about Basecamp, and realized many of those arguments applied to my situation, given my values, and -- after a lot of reflection -- I changed my mind. I think Basecamp itself is mostly closed source, so they may have an advantage in building a business. SageMathCloud (and SageMath) really are 100% open source, and building a completely open source business might be harder. Our open source IP is considered worthless by investors. Witness: RethinkDB just shut down and Stripe hired just the engineers -- all the IP, customers, etc., of RethinkDB was evidently considered worthless by investors.The day after the A16Z meeting, I met with my board, which went well (we discussed a huge range of topics over several hours). Some of the board members also tried hard to convince me that I should raise a lot more investor money.
Will Poole: you're doomed
Two weeks ago I met with Will Poole, who is a friend of a friend, and we talked about my company and plans. I described what I was doing, that everything was open source, that I was incentivizing the company around building a business rather than raising investor money. He listened and asked a lot of follow up questions, making it very clear he understands building a company very, very well.His feedback was discouraging -- I said "So, you're saying that I'm basically doomed." He responded that I wasn't doomed, but might be able to run a small "lifestyle business" at best via my approach, but there was absolutely no way that what I was doing would have any impact or pay for my kids college tuition. If this was feedback from some random person, it might not have been so disturbing, but Will Poole joined Microsoft in 1996, where he went on to run Microsoft's multibillion dollar Windows business. Will Poole is like a retired four-star general that executed a successful campaign to conquer the world; he been around the block a few times. He tried pretty hard to convince me to make as much of SageMathCloud closed source as possible, and to try to convince my users to make content they create in SMC something that I can reuse however I want. I felt pretty shaken and convinced that I needed to close parts of SMC, e.g., the new Kubernetes-based backend that we spent all summer implementing. (Will: if you read this, though our discussion was really disturbing to me, I really appreciate it and respect you.)
My friend, who introduced me to Will Poole, introduced me to some other people and described me as that really frustrating sort of entrepreneur who doesn't want investor money. He then remarked that one of the things he learned in business school, which really surprised him, was that it is good for a company to have a lot of debt. I gave him a funny look, and he added "of course, I've never run a company".
I left that meeting with Will convinced that I would close source parts of SageMathCloud, to make things much more defensible. However, after thinking things through for several days, and talking this over with other people involved in the company, I have chosen not to close anything. This just makes our job harder. Way harder. But I'm not going to make any decisions based purely on fear. I don't care what anybody says, I do not think it is impossible to build an open source business (I think Wordpress is an example), and I do not need to raise VC.
Hacker News Discussion: https://news.ycombinator.com/item?id=12663599
Chinese version: http://www.infoq.com/cn/news/2016/10/Reflection-sustainable-profit-co
↧
Lauren Devitt: Improbable by Number
As a Mathematician I enjoy reading non-fiction that is not too "mathy", one that makes subjects such as probability approachable. This is the first in a series of reviews of books I've been reading for fun and for my math history course. These reviews will high light some of the more interesting parts of the book as well as rate how approachable the book made the subject and how educational on the subject the books really are.
The first book I am Reviewing is The Improbability Principle by
↧
↧
Lauren Devitt: Logicomix- logic by number
A book review of Logicomix. Written by Apostolos Doxiadis and Christos H. Papadimitriou. Art by Alecos Papadatos and Annie Di Donna.
This is the first graphic novel I've ever read. I had no idea mathe history graphic novels was a genre. I've justs tarted reading my second about Ada lovelace and Charles Babbage. Logicomix is primarily abourt Bertrand Russell, creator of russells paradox. it is written from the view of the authors and artisits of the novel as well as switching to whats going on
↧
Lauren Devitt: Books by Number- The Number Devil
This is the post content
↧
Sébastien Labbé: A time evolution picture of packages built in parallel by Sage
Compiling sage takes a while and does a lot of stuff. Each time I am wondering which components takes so much time and which are fast. I wrote a module in my slabbe version 0.3b2 package available on PyPI to figure this out.
This is after compiling 7.5.beta6 after an upgrade from 7.5.beta4:
sage:fromslabbe.analyze_sage_buildimportdraw_sage_buildsage:draw_sage_build().pdf()
From scratch from a fresh git clone of 7.5.beta6, after running MAKE='make-j4' make ptestlong, I get:
sage:fromslabbe.analyze_sage_buildimportdraw_sage_buildsage:draw_sage_build().pdf()
The picture does not include the start and ptestlong because there was an error compiling the documentation.
By default, draw_sage_build considers all of the logs files in logs/pkgs but options are available to consider only log files created in a given interval of time. See draw_sage_build? for more info.
↧
Lauren Devitt: Grapic Novels by Number
Feynman
Turing
Russell- Logicomix
↧
↧
Liang Ze: Distributive Laws
I’ve been participating in the Kan Extension Seminar II, and this week it’s my turn to post about Jon Beck’s “Distributive Laws” at the n-Category Cafe!
The post uses lots of string diagrams for monads, resulting in pictures like the following:
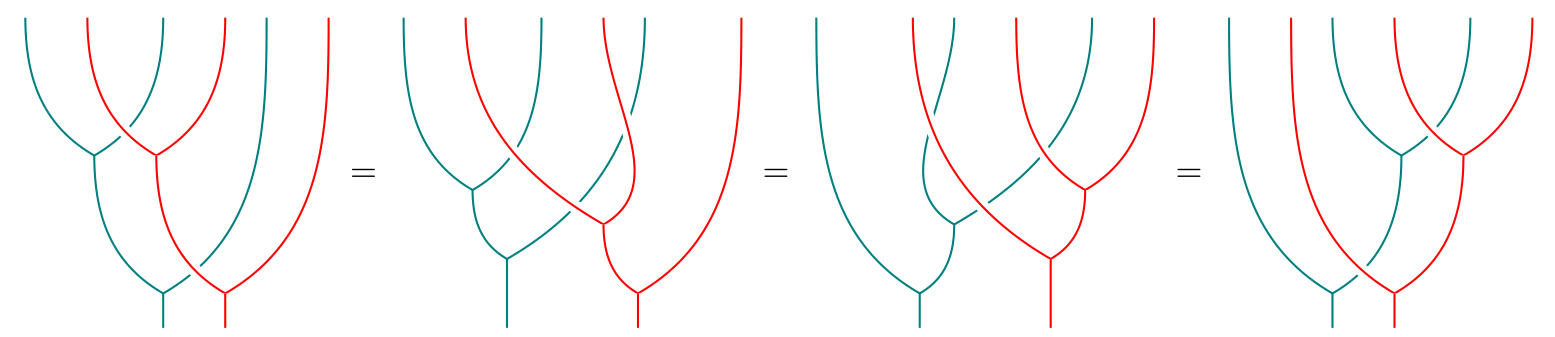
See you there!
↧
Harald Schilly: SageMath GSoC 2017 Projects
6 GSoC SageMath Projects
During the past couple of summers, SageMath successfully managed many Google Summer of Code projects. This year we are again happy to have six projects:Implementing matroid classes and plotting improvements
(Zachary Gershkoff / Stefan van Zwam)This project seeks to implement several common matroid classes in SageMath, along with algorithms for their display and relevant computations. The graphic matroid class in particular will be implemented with a representative graph with methods for Whitney switching and minor operations. This will be accompanied by improvements to the graph theory library, with methods relevant to matroids enabled to support multigraphs. Other modules for this project include improved plotting of rank 3 matroids to eliminate false colinearities, computation of a matroid's automorphism group using SageMath's group theory libraries, and faster minor testing based on an existing trac ticket.
Expanding the Functionality of Dynamical Systems
(Rebecca Lauren Miller / Paul Fili and Ben Hutz)
As a member of the sage-dynamics community, researchers have compiled a wishlist for algorithms and functionality they would like added. I would like to shorten the wish list for us.For my project I will be completing some desired additions to SAGE from the Sage Dynamics Wiki. I will implement Well’s Algorithm, strengthen the numerical precision in cannonical_height, as well as implement reduced_form for higher dimensions.
Improvement of Complex Dynamics in Sage
(Ben Barros / Adam Towsley and Ben Hutz)
There are three major things that I would like to implement to improve the functionality of Sage in the area Complex Dynamics. The details of the project are summarized in the following list:
- Complex Dynamics Graphical package: Integrate or implement a complex dynamics software such as Mandel into Sage. This will be done by creating an optional package for Sage. If there is enough demand, the package may become a standard package for Sage at some point.
- Spider Algorithm: The object of the Spider Algorithm is to construct polynomials with assigned combinatorics. For example, we may want to find a polynomial that has a periodic orbit of period 7. The Spider Algorithm provides a way for us to compute this polynomial efficiently. I plan to implement this algorithm into Sage.
- Coercion: If you have a map defined over Q, you should be able to take the image of a point over C (i.e. somewhere you have a well-defined embedding) without having to use the command "change_ring()". Something similar works for polynomials in Sage but it does not work for morphisms/schemes.
Linear-time Implementation of Modular Decomposition of Undirected and Directed Graphs
(Lokesh Jain / Dima Pasechnik)
This project is aimed at providing linear time implementation for modular decomposition of graphs and digraphs. Modular decomposition is decomposition of graph into modules. A module is a subset of vertices and it is a generalization of connected component in graph. Let us take for example a module X. For any vertex v ∉ X it is either connected or not connected to every vertex of X. Another property of module is that a module can be subset of another module. There are various algorithms which have been published for modular decomposition of graphs. The focus in this project is on linear time complexity algorithms which can be practically implemented. The project further aims to use the modules developed for modular decomposition to implement other functionality like skew partitions. Skew partition is partition of graph into two sets of vertices such that induced graph formed by one set is disconnected and induced graph formed by other set is complement of the first. Modular decomposition is a very important concept in Graph Theory and it has a number of use cases. For instance it has been an important tool for solving optimization and combinatorics problems.
Modular Decomposition of graphs and digraphs
(Maria Ioanna Spyrakoy / Dima Pasechnik)
Modular decomposition of (di)graphs is a generalization of the concept of the decomposition of (di)graphs into connected components. Its current implementation in Sage relies on badly broken abandoned C code, and badly needs to be replaced by something that works and is not too slow. However, the only open-source implementations of some of these procedures are either in Java or in Perl, and thus aren't really useful for Sage.
Note: A attentive reader might notice the similarity between those projects. They will be split regarding the type of graph and be coordinated to not overlap but to augment each other.
Visualizing constructs in cluster algebras and quiver representations
(Bryan Wang / Travis Scrimshaw)
I aim to implement visualizations of several key constructs in cluster algebras and quiver representations. The first is Auslander-Reiten quivers, for at least the A_n and D_n cases. The second is labelled endomorphism quivers and mutations within a cluster category, focusing on the A_n case. The third is posets of down-mutations for the A_n case. These features will be useful not only for research purposes, but also as nice examples to play around with and learn from. Aside from these features, I am interested in implementing features for the Quantum Cluster Algebras project.
All the best for this summer, thank you to Google for making this possible, and sorry to all those candidates who didn't make it ...
↧
OpenDreamKit: OOMMF Python interface presentation
Hans Fangohr presented the first prototype of the Python OOMMF interface at the 61st international meeting on magnetism and magnetic materials in New Orleans (US).
↧