Although I gave a brief exposition of the "baseline" explicit formula for the elliptic curve $L$-functions in a previous post, I wanted to spend some more time showing how one can use this formula to prove some useful statements about the elliptic curves and their $L$-functions. Some of these are already implemented in some way in the code I am building for my GSoC project, and I hope to include more as time goes on.
First up, let's fix some notation. For the duration of this post we fix an elliptic curve $E$ over the rationals with conductor $N$. Let $L_E(s)$ be its associated $L$-function, and let $\Lambda_E(s)$ be the completed $L$-function thereof, i.e.
$\Lambda_E(s) = N^{s/2}(2\pi)^s\Gamma(s)L_E(s)$, where $\Gamma$ is the usual Gamma function on $\mathbb{C}$. If you want to know more about how $E$, $L_E$ and $\Lambda_E$ are defined and how we compute with them, some of my previous posts (
here and
here) go into their exposition in more detail.
Let's recap briefly how we derived the baseline explicit formula for the $L$-function of $E$ (see
this post for more background thereon). Taking logarithmic derivatives of the above formula for $\Lambda_E(s)$ and shifting to the left by one gives us the following equality:
$$\frac{\Lambda_E^{\prime}}{\Lambda_E}(1+s) = \log\left(\frac{\sqrt{N}}{2\pi}\right) + \frac{\Gamma^{\prime}}{\Gamma}(1+s) + \frac{L_E^{\prime}}{L_E}(1+s).$$
Nothing magic here yet. However, $\frac{\Lambda_E^{\prime}}{\Lambda_E}$, $\frac{\Gamma^{\prime}}{\Gamma}$ and $\frac{L_E^{\prime}}{L_E}$ all have particularly nice series expansions about the central point. We have:
- $\frac{\Lambda_E^{\prime}}{\Lambda_E}(1+s) = \sum_{\gamma} \frac{s}{s^2+\gamma^2}$, where $\gamma$ ranges over the imaginary parts of the zeros of $L_E$ on the critical line; this converges for any $s$ not equal to a zero of $L_E$.
- $\frac{\Gamma^{\prime}}{\Gamma}(1+s) = -\eta + \sum_{k=1}^{\infty} \frac{s}{k(k+s)}$, where $\eta$ is the Euler-Mascheroni constant $=0.5772156649\ldots$ (this constant is usually denoted by the symbol $\gamma$ - but we'll be using that symbol for something else soon enough!); this sum converges for all $s$ not equal to a negative integer.
- $\frac{L_E^{\prime}}{L_E}(1+s) = \sum_{n=1}^{\infty} c_n n^{-s}$; this only converges absolutely in the right half plane $\Re(s)>\frac{1}{2}$.
Here
$$ c_n = \begin{cases}
\left[p^m+1-\#E(\mathbb{F}_{p^m})\right]\frac{\log p}{p^m}, & n = p^m \mbox{ is a perfect prime power,} \\
0 & \mbox{otherwise.}\end{cases} $$
Assembling these equalities gives us the aforementioned explicit formula:
$$ \sum_{\gamma} \frac{s}{s^2+\gamma^2} = \left[-\eta+\log\left(\frac{\sqrt{N}}{2\pi}\right)\right] + \sum_{k=1}^{\infty} \frac{s}{k(k+s)} + \sum_n c_n n^{-s}$$
which holds for any $s$ where all three series converge. It is this formula which we will use repeatedly to plumb the nature of $E$.
For ease of exposition we'll denote the term in the square brackets $C_0$. It pitches up a lot in the math below, and it's a pain to keep writing out!
Some things to note:
- $C_0 = -\eta+\log\left(\frac{\sqrt{N}}{2\pi}\right)$ is easily computable (assuming you know $N$). Importantly, this constant depends only on the conductor of $E$; it contains no other arithmetic information about the curve, nor does it depend in any way on the complex input $s$.
- The sum $\sum_{k=1}^{\infty} \frac{s}{k(k+s)}$ doesn't depend on the curve at all. As such, when it comes to computing values associated to this sum we can just hard-code the computation before we even get to working with the curve itself.
- The coefficients $c_n$ can computed by counting the number of points on $E$ over finite fields up to some bound. This is quick to do for any particular prime power.
Good news: the code I've written can compute all the above values quickly and efficiently:
sage: E = EllipticCurve([-12,29])
sage: Z = LFunctionZeroSum(E)
sage: N = E.conductor()
sage: print(Z.C0(),RDF(-euler_gamma+log(sqrt(N)/(2*pi))))
(2.0131665172, 2.0131665172)
sage: print(Z.digamma(3.5),RDF(psi(3.5)))
(1.10315664065, 1.10315664065)
sage: Z.digamma(3.5,include_constant_term=False)
1.68037230555
sage: Z.cn(389)
-0.183966457901
sage: Z.cn(next_prime(1e9))
0.000368045198812
sage: timeit('Z.cn(next_prime(1e9))')
625 loops, best of 3: 238 µs per loop
So by computing values on the right we can compute the sum on the left - without having to know the exact locations of the zeros $\gamma$, which in general is hard to compute.
Now that we have this formula in the bag, let's put it to work.
NAÏVE RANK ESTIMATION
If we multiply the sum over the zeros by $s$ and letting $\Delta = 1/s$, we get
$$\sum_{\gamma} \frac{\Delta^{-2}}{\Delta^{-2}+\gamma^2} = \sum_{\gamma} \frac{1}{1+(\Delta\gamma)^2},$$
Note that for large values of $\Delta$, $\frac{1}{1+(\Delta\gamma)^2}$ is small but strictly positive for all nonzero $\gamma$, and 1 for the central zeros, which have $\gamma=0$. Thus the value of the sum when $\Delta$ is large gives a close upper bound on the analytic rank $r$ of $E$. That is, we can bound the rank of $E$ from above by choosing a suitably large value of $\Delta$ and computing the quantity on the right in the inequality below:
$$r < \sum_{\gamma} \frac{1}{1+(\Delta\gamma)^2} = \frac{1}{\Delta}\left[C_0 + \sum_{k=1}^{\infty} \frac{1}{k(1+\Delta k)} + \sum_n c_n n^{-1/\Delta}\right]. $$
Great! Right? Wrong. In practice this approach is not a very good one. The reason is the infinite sum over $n$ only converges absolutely for $\Delta<2$, and for Delta values as small as this, the obtained bound won't be very good. A value of $\Delta=2$, for example, gives us the zero sum $\sum_{\gamma} \frac{1}{1+(2\gamma)^2}$. If a curve's $L$-function has a zero with imaginary part about 0.5, for example - as many $L$-functions do - then such a zero will contribute 0.5 to the sum. And because zeros come in symmetric pairs, the sum value will then be at least a whole unit larger than the actual analytic rank. In general, for $\Delta<2$ the computed sum can be quite a bit bigger than the actual analytic rank of $E$.
Moreover, even though the Generalized Riemann Hypothesis predicts that the sum $\sum_n c_n n^{-1/\Delta}$ does indeed converge for any positive value of $\Delta$, in practice the convergence is so slow that we end up needing to compute inordinate amounts of the $c_n$ in order to hope to get a good approximation of the sum. So no dice; this approach is just too inefficient to be practical.
![]() |
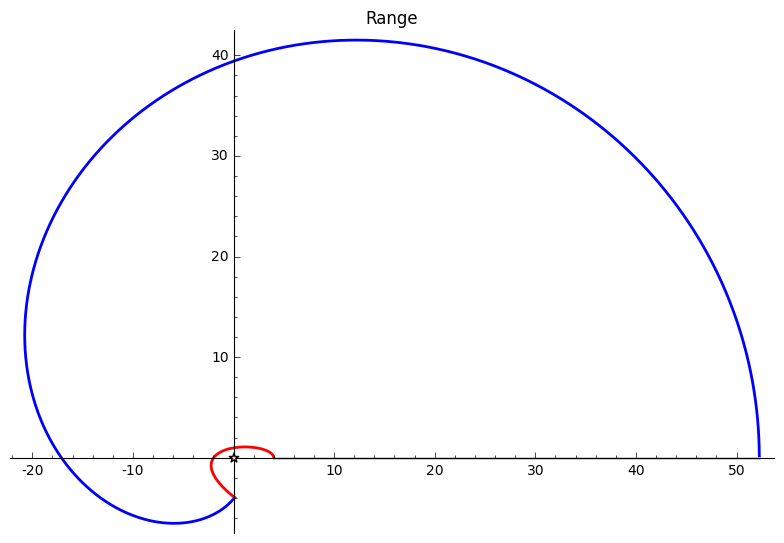
| A graphic depiction of the convergence problems we run into when trying to evaluate the sum over the $c_n$. For the elliptic curve $E: y^2 + y = x^3 - 79*x + 342$ the above plot shows the cumulative sum $\sum_{n<T} c_n n^{-1/4}$ for $T$ up to 100000; this corresponds to $\Delta=4$. Note that even when we include this many terms in the sum, its value still varies considerably. It's unlikely the final computed value is correct to a single decimal digit yet. |
A BETTER APPROACH (THE ONE IMPLEMENTED IN MY CODE)
We can get around this impasse by evaluating a modified sum over the zeros, one which requires us to only ever need to compute finitely many of the $c_n$. Here's how we do it. Start with the sum $\sum_{\gamma} \frac{s}{s^2+\gamma^2}$, and divide by $s^2$ to get $\frac{1}{s(s^2+\gamma^2)}$. Now hearken back to your college sophomore math classes and take the inverse Laplace transform of this sum. We get
$$ \mathcal{L}^{-1} \left[\sum_{\gamma} \frac{1}{s(s^2+\gamma^2)}\right](t) = \sum_{\gamma} \mathcal{L}^{-1} \left[\frac{1}{s(s^2+\gamma^2)}\right](t) = \frac{t^2}{2} \sum_{\gamma} \left(\frac{\sin(\frac{t}{2}\gamma)}{\frac{t}{2}\gamma}\right)^2 $$
Letting $\Delta = \frac{t}{2\pi}$ we get the sum
$$ \mathcal{L}^{-1} \left[\sum_{\gamma} \frac{s}{s^2+\gamma^2}\right](\Delta) = 2\pi^2\Delta^2 \sum_{\gamma} \text{sinc}^2(\Delta\gamma), $$
where $\text{sinc}(x) = \frac{\sin(\pi x)}{\pi x}$, and $\text{sinc}(0) = 1$.
Note that as before, $\text{sinc}^2(\Delta\gamma)$ exaluates to 1 for the central zeros, and is small but positive for all nonzero $\gamma$ when $\Delta$ is large. So again, this sum will give an upper bound on the analytic rank of $E$, and that this bound converges to the true analytic rank as $\Delta \to \infty$.
If we do the same - divide by $s^2$ and take inverse Laplace transforms - to the quantities on the right, we get the following:
- $\mathcal{L}^{-1} \left[\frac{C_0}{s^2} \right] = 2\pi\Delta C_0;$
- $ \mathcal{L}^{-1} \left[\sum_{k=1}^{\infty} \frac{1}{sk(k+s)}\right] = \sum_{k=1}^{\infty} \frac{1}{k^2}\left(1-e^{-2\pi\Delta k}\right);$
- $\mathcal{L}^{-1} \left[ \sum_{n=1}^{\infty} c_n \frac{n^{-s}}{s^2} \right] = \sum_{\log n<2\pi\Delta} c_n\cdot(2\pi\Delta - \log n). $
Note that the last sum is
finite: for any given value of $\Delta$, we only need to compute the $c_n$ for $n$ up to $e^{2\pi\Delta}$. This is the great advantage here: we can compute the sum
exactly without introducing any truncation error. The other two quantities are also readly computable to any precision.
Combining the above values and dividing by $2\pi^2\Delta^2$, we arrive at the rank bounding formula which is implemented in my GSoC code, hideous as it is:
\begin{align*}
r < \sum_{\gamma} \text{sinc}^2(\Delta\gamma) = \frac{1}{\pi\Delta} &\left[ C_0 + \frac{1}{2\pi\Delta}\sum_{k=1}^{\infty} \frac{1}{k^2}\left(1-e^{-2\pi\Delta k}\right) \right. \\
&\left. + \sum_{n<e^{2\pi\Delta}} c_n\left(1 - \frac{\log n}{2\pi\Delta}\right) \right] \end{align*}
Of course, the number of terms needed on the right hand side is still exponential in $\Delta$, so this limits the tightness of the sum we can compute on the left hand side. In practice a personal computer can compute the sum with $\Delta=2$ in a few seconds, and a more powerful cluster can handle $\Delta=3$ in a similar time. Beyond Delta values of about 4, however, the number of $c_n$ is just too great to make the sum effectively computable.
THE DENSITY OF ZEROS ON THE CRITICAL LINE
Explicit formula-type sums can also be used to answer questions about the distribution of zeros of $L_E$ along the critical line. Let $T$ be a positive real number, and $M_E(T)$ be the counting function that gives the number of zeros in the critical strip with imaginary part at most $T$ in magnitude. By convention, when $T$ coincides with a zero of $L_E$, then we count that zero with weight. In other words, we can write
$$ M_E(T) = \sum_{|\gamma|<T} 1 + \sum_{|\gamma|=T} 1/2.$$
There is a more mathematically elegant way to write this sum. Let $\theta(x)$ be the Heaviside function on $x$ given by
$$ \theta(x) = \begin{cases} 0, & x<0 \\
\frac{1}{2}, & x=0 \\
1, & x>0. \end{cases}$$
Then we have that
$$M_E(T) = \sum_{\gamma} \theta(T^2-\gamma^2). $$
We have written $M_E(T)$ as a sum over the zeros of $L_E$, so we expect that it comprises the left-hand-side of some explicit formula-type sum. This is indeed this the case. Using Fourier transforms we can show that
$$M_E(T) = \frac{2}{\pi}\left[C_0 T + \sum_{k=1}^{\infty} \left(\frac{T}{k} - \arctan \frac{T}{k}\right) + \sum_{n=1}^{\infty} \frac{c_n}{\log n}\cdot \sin(T\log n) \right] $$
With this formula in hand we can start asking questions on how the zeros of $L_E$ are distributed. For example, how does average zero density on the critical line scale as a function of $T$, the imaginary part of the area in the critical strip we're considering? How does zero density scale with the curve's conductor $N$?
If one assumes the Generalized Riemann Hypothesis, we can show that $\sum_{n=1}^{\infty} \frac{c_n}{\log n}\cdot \sin(T\log n) = O(\log T)$. Moreover, this sum is in a sense equidistributed about zero, so we expect its contribution for a sufficiently large randomly chosen value of $T$ to be zero. The other two quantities are more straightforward. The $C_0 T$ term is clearly linear in $T$. Going back to the definition of $C_0$, we see that $C_0 T = \frac{1}{2}T\log N + $constant$\cdot T$. Finally, we can show that the sum over $k$ equals $T\log T + O(\log T)$. Combining this gives us the estimate
$$ M_E(T) = \frac{1}{\pi} T (\log N + 2\log T+a) + O(\log T) $$
for some explicitly computable constant $a$ independent of $E$, $N$ or $T$ . That is, the number of zeros with imaginary part at most $T$ in magnitude is "very close" to $\frac{1}{\pi}T(\log N + 2\log T)$. Another way to put it is than the number of zeros in the interval $[T,T+1]$ is about $\frac{1}{2}\log N + \log T$.
![]() |
The value of $M_E(T)$ for $T$ up to 30, for the elliptic curve $E: y^2 + y = x^3 - x$. The black line is just the 'smooth part' of $M_E(T)$, given by $\frac{2}{\pi}\left(C_0 T + \sum_{k=1}^{\infty} \left(\frac{T}{k} - \arctan \frac{T}{k}\right)\right)$. This gives us the 'expected number of zeros up to $T$', before we know any data about $E$ other than its conductor. The blue line is what we get when we add in $\sum_{n=1}^{\infty} \frac{c_n}{\log n}\cdot \sin(T\log n)$, which tells us the exact locations of the zeros: they will be found at the places where the blue curve jumps by 2.
Note that the sum over $n$ converges *very* slowly. To produce the above plot, I included terms up to $n=1 000 000$, and there is still considerable rounding visible in the blue curve. If I could some how evaluate the $c_n$ sum in all its infinite glory, then resulting plot would be perfectly sharp, comprised of flat lines that jump vertically by 2 at the loci of the zeros. |
These are two of the uses of explicit formula-type sums in the context of elliptic curve $L$-functions. If you want to read more about them, feel free to pick up my PhD thesis - when it eventually gets published!
(think of a vector space, but only integer linear combinations are allowed) is hard. The main tool for finding such short vectors is lattice reduction. 
longer than the actually shortest vector in the lattice (read: not so good). This is good enough for many applications but not good enough to, e.g. solve LWE. 
where σ is the width parameter (close to the standard deviation) and c is the centre. There are several algorithms to choose from to sample from such a distribution each being better or worse in some situations. Somewhat surprisingly, though, when I got started implementing some lattice-based crypto there was no ![\mathbb{Z}[x]/(x^n+1)](http://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5Bx%5D%2F%28x%5En%2B1%29&bg=eeebf2&fg=3c3d47&s=0 "\mathbb{Z}[x]/(x^n+1)")
, where n is a power of two, and with all operations in quasi-linear time. While the code is already fairly modular, i.e. we separated crypto applications from arithmetic, it might make sense to outsource this module into a separate library so it can used more easily by other projects should they wish to. 
, i.e. the field with two elements 0 and 1. We released one ![\mathbb{F}_2[x]/f(x)](http://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_2%5Bx%5D%2Ff%28x%29&bg=eeebf2&fg=3c3d47&s=0 "\mathbb{F}_2[x]/f(x)")
where f(x) is an irreducible polynomial over ![\mathbb{F}_2[x]](http://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_2%5Bx%5D&bg=eeebf2&fg=3c3d47&s=0 "\mathbb{F}_2[x]")
of degree up to 16. We released one 
and 
which comes in handy from time to time. SCIP is open source in the sense that you can read the source code, but its license does not live up the standards of the 
