I’ve recently been playing a really cool video game: Vainglory. This is described as a MOBA which I must admit I had never heard off until this year when my students mentioned it to me, but basically it’s an online multi player game in which players form two teams of 6 heroes and fight each other. The choice of the heroes is very important as the composition of a team can make or break a match. This seems to have a bit of a cult following (so no doubt just like for my post about clash of clans I might annoy people again) and there is a great wiki that gives guides for the play of each player. In this post I’ll describe using Python to scrape that wiki to get data that feeds in to a game theoretic model which I then analyse using Sagemath to give some insight about the choice of hero.

Here’s the map where this all takes place:

So first of all, my understanding is that there are generally three types of playing strategy in the game:

• Lane: a hero that occupies and tries to take over the main route between the two bases.
• Jungle: a hero that goes ‘off road’ and kills monsters, gets gold etc…
• Roam: a hero who roams in between the two and whose main job is to support the other two players.

My personal strategy is to pick a roamer/protector: Ardan (pic below),

I generally help out the jungler in my team and try my best to not be a liability by dying.

The wiki has a bunch of information for players. If you google something like ‘vainglory best strategy’ it comes up. If you look up each hero you get a collection of guides ranked by votes each with all sorts of information which includes the where each and every other hero sits on a threat level (from 1 to 10). Here is the threat meter for Ardan from the top guide:

So from that guide it looks like if your opponent is going to be isolated with Ardan then you should pick HERO. In some guides the threat meter does not list all the heros. This is particularly important as it’s these threat meters that I’ve used as a source of data for how good a given hero is against other heros.

This is where the keener player/reader will note that the threat meter only describes the threat to a single player and not any information about how this fits within a team dynamic. This is an important admission on my part: as indicated by the title of this post aims to use data and game theory to give an indication as to how to choose heros for isolated combat against other single heros. So one application of this is choosing a jungler/laner when you expect to go up against another team that is playing a single jungler/laner.

Scraping the data

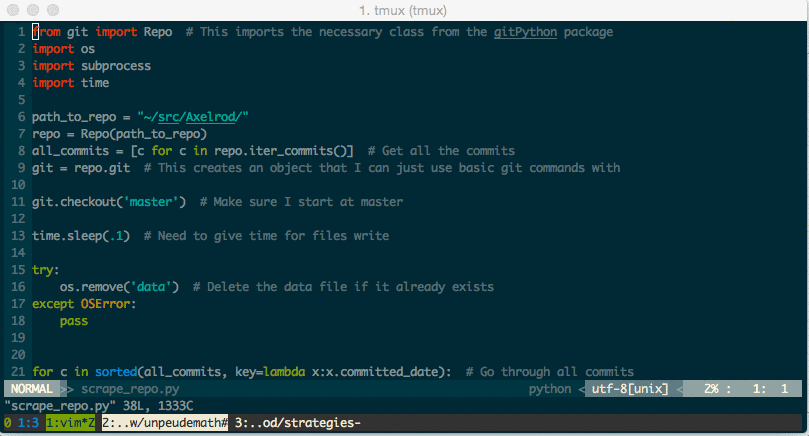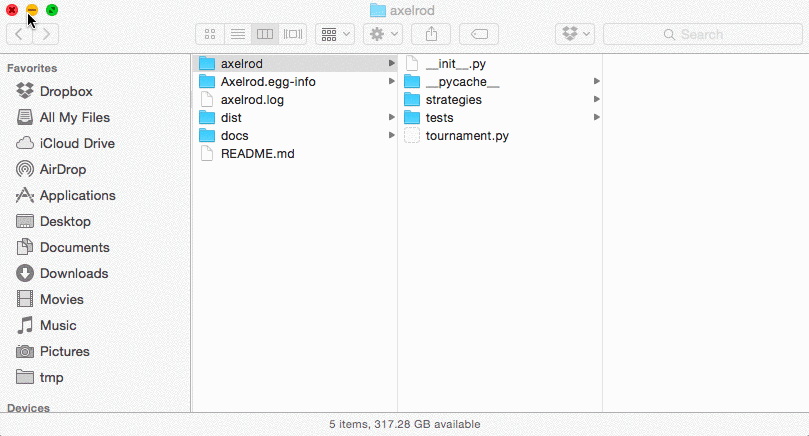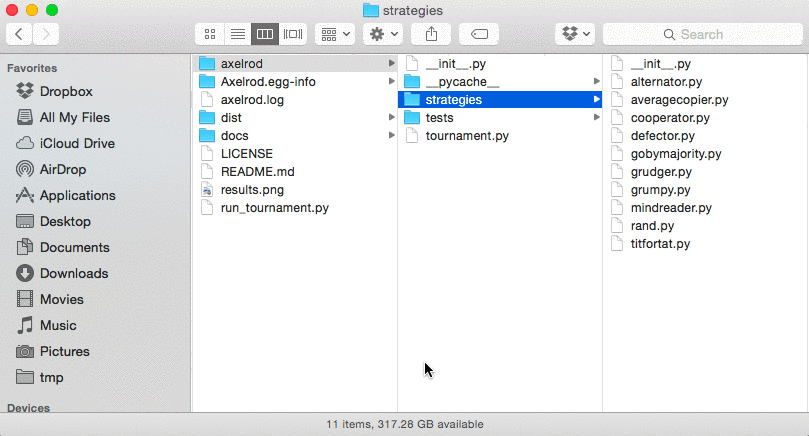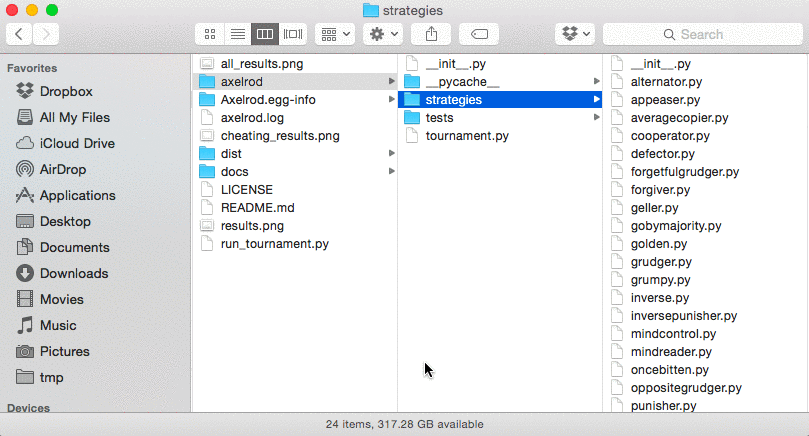
First things first: I used Python with the BeautifulSoup and requests library. For example here is how I got the lists of all the heroes (and the url to their own respective page on the wiki):

>>>page=requests.get('http://www.vaingloryfire.com/vainglory/wiki/heroes')>>>soup=BeautifulSoup(page.text,'html.parser')>>>root='/vainglory/wiki/heroes'>>>urls=[link.get('href')forlinkinsoup.find_all('a')]>>>heroes={url[len(root)+1:]:urlforurlinurls[2:]ifurl.startswith(root+'/')}>>>delheroes['skye']# Removing skye as she is brand new{u'adagio':u'/vainglory/wiki/heroes/adagio',u'ardan':u'/vainglory/wiki/heroes/ardan',u'catherine':u'/vainglory/wiki/heroes/catherine',u'celeste':u'/vainglory/wiki/heroes/celeste',u'fortress':u'/vainglory/wiki/heroes/fortress',u'glaive':u'/vainglory/wiki/heroes/glaive',u'joule':u'/vainglory/wiki/heroes/joule',u'koshka':u'/vainglory/wiki/heroes/koshka',u'krul':u'/vainglory/wiki/heroes/krul',u'petal':u'/vainglory/wiki/heroes/petal',u'ringo':u'/vainglory/wiki/heroes/ringo',u'rona':u'/vainglory/wiki/heroes/rona',u'saw':u'/vainglory/wiki/heroes/saw',u'skaarf':u'/vainglory/wiki/heroes/skaarf',u'taka':u'/vainglory/wiki/heroes/taka',u'vox':u'/vainglory/wiki/heroes/vox'}

(Note there that I’m removing a brand new hero: Skye as she was released pretty much at the same time as I was writing this post.)

You can see the JuPyTer notebook which shows the code. The main technicality is that I only scraped guides from the front page for each hero. As I’ll describe later, I ran my analysis taking the average threats for a variety of cases: only taking the first guide, only taking the first 2 guides, the first 3 guides etc…

Here for example is the threats data for Adagio if you only look at this first guide:

[0,0,0,0,0,0,4,0,0,0,4,0,0,7,0,0]

Cross referencing that with the order given by the list of heroes above we see that Skaarf ranks a 7 on the threat meter to Adagio, and Ringo and Joule a 4. All the 0s are what I’ve decided to do when a threat meter does not include a given hero: indicating that that hero is not a threat to that hero. I don’t really like this as a solution but it’s probably the least worst way to deal with it (if anyone has a better way of handling this please let me know in the comments).

Here is the threats data for Krul:

[6,3,4,3,6,4,3,7,5,5,4,0,6,6,5,0]

We see that in this case the only heroes that pose no threat to Krul are Fortress and Rona. Thus if your opponent is playing those heroes Krul is a best response.

As will be described in the next section, we need to build up a matrix of these rows which basically shows how well a given hero does against others. Here is the matrix of this when considering the row players and taking the opposite of the threats when using just the top guide:

If you consider a column (that corresponds to a hero) of that matrix, the row player aims to find the row that gives the highest score, which because we’ve taken the opposite of the threat score corresponds to minimising the threat posed by the column hero. This is in essence a risk averse approach, at the very end I’ll comment on what happens to the results when players aim to maximise the threat they pose.

Now that I’ve described the data (you can find all the data written to specific csv files here) I’ll go on to talk about the game theory used to try and see what the equilibrium choice of strategies should/could be.

Game theoretic analysis

All of this has been done using Sagemath, a great open source mathematics package that offers an alternative to Maple, Mathematica etc…

If you’re not familiar with game theory, this video might help (it shows the basics of game theory and how Sagemath can be used to find Nash equilibria):

Before talking about equilibria let’s just look at best response dynamics.

Using Sage we can first of all build up the normal form game for a given number of guides:

sage:defbuild_game(row_player_file,col_player_file):....:"""Import the bi matrices and create the game object"""....:bi_matrices=[]....:forflein[row_player_file,col_player_file]:....:f=open(fle,'r')....:csvrdr=csv.reader(f)....:bi_matrices.append(-matrix([[float(ele)foreleinrow]forrowincsvrdr]))....:f.close()....:....:returnNormalFormGame(bi_matrices)sage:g=build_game("A-01.csv","B-01.csv")

Using this and the best_response method on Sagemath NormalFormGames we can build up all the best responses (according to a given number of guides) go each player. The cool thing is that Sagemath has some awesome graph theory written in there so we can transform that in to a nice picture (again: all the code for this can be found here):

That plot confirms what we have seen earlier, we see that Krul is a best response to Fortress or Rona. Sadly, because there are so many zeros when just using the first guide, there are a bunch of heros that are not considered a threat to any of the players so they have multiple best responses and our graph is messy.

Here is the best response graph when taking the mean threats over all front page guides:

Note that Game Theory assumes that everyone know that everyone know that everyone knows… all this. So for example if two players both player Adagio we are at an equilibrium. However if one player plays Saw then the graph indicates that the opponent should play Koshka, which means that the first player should then deviate and play Fortress which is then also an equilibrium (bot players are playing best responses to each other).

From here on I will continue the analysis using the average utility from all the guides (I’ll come back to this at the end).

So we can use Sagemath to compute all the equilibria for us. A Nash equilibria need not be a pure strategy and so will at times be a probability vector indicating how players should randomly pick a hero. Here for example is the 4th equilibrium computed by Sagemath:

sage:g.obtain_nash(algorithm='lrs')[3][(0,0,0,0,0,0,0,0,3947/17781,0,3194/17781,0,8795/17781,0,0,615/5927),(0,0,0,0,0,0,0,0,3947/17781,0,3194/17781,0,8795/17781,0,0,615/5927)]

This particular equilibria has both players playing a mix of: Fortress, Glaive, Petal and Koshka.

Here is the mean probability distribution for both players, while the particular values should be ignored what is of interest is the heroes that are not played at all. In essence these heroes, accross all the equilibria are not deemed playable:

We see that this confirms how the previous graph was colored showing the heroes that should be played in blue.

Note that the number of guides and the reliability of all this has a huge effect of the conclusions made. Here are two gifs that show the effect of the number of guides used:

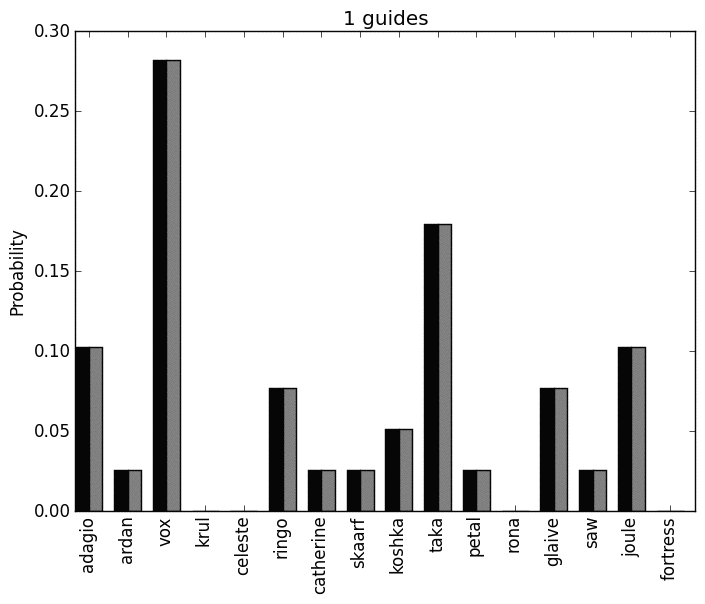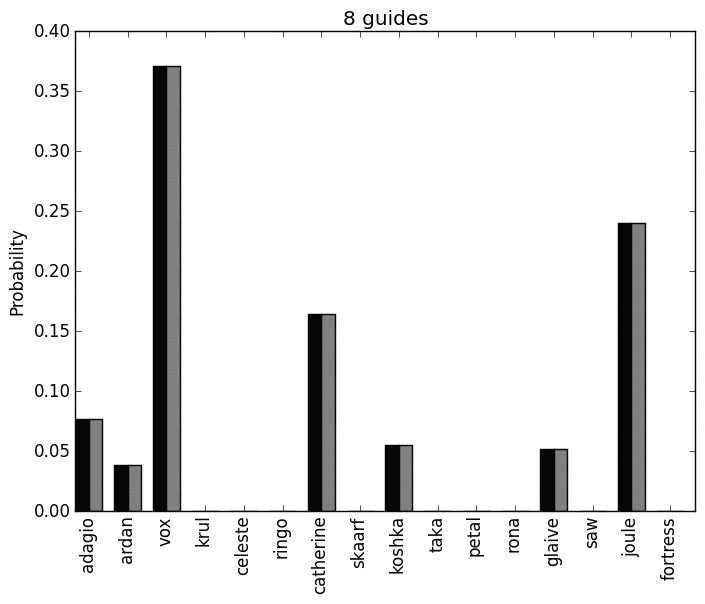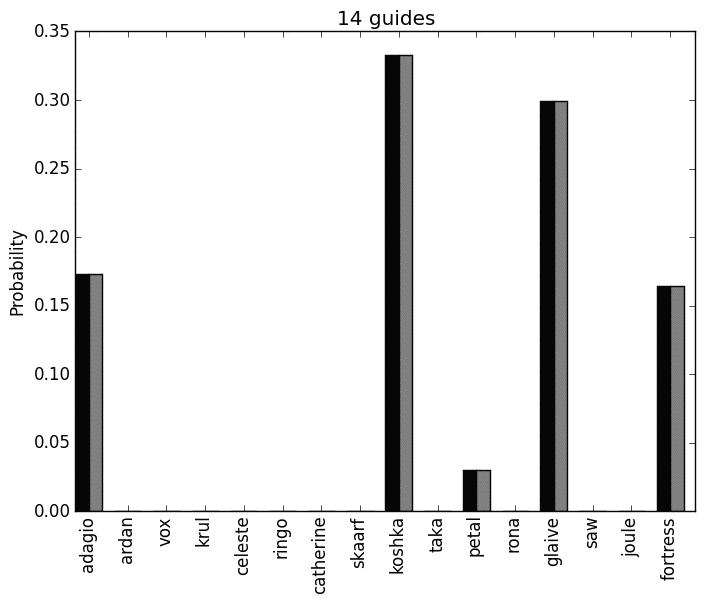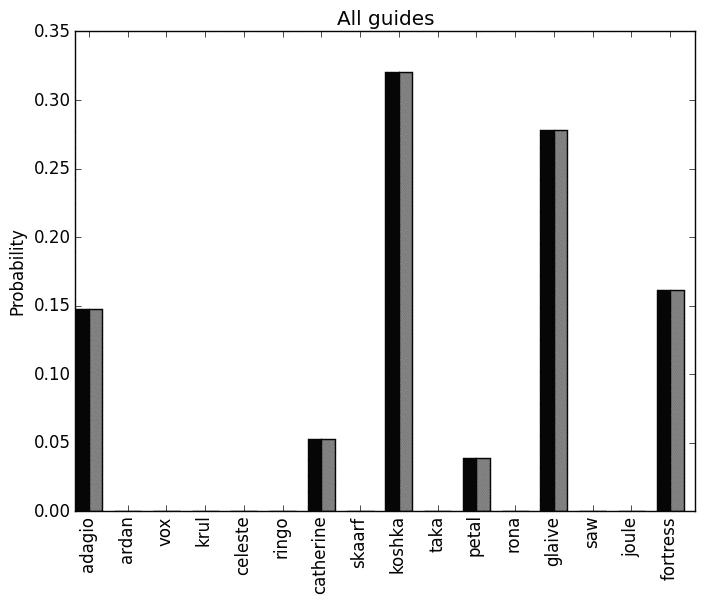
and here is a plot of the number of equilibria for each guide:

Up until now all the results are for when players aim to minimise the threat posed to them. In the next section I’ll invert that (python wise it’s a minor swapping around of some inputs) and consider the situation where you want to pick a hero that is aims to be the most threatening.

Seeking to be a threat

First of all here is the best response graph:

Here is the average of the NE:

Those 3 players have certainly been able to rip through me on more than one occasion…

Finally here are the Nash equilibria for when a threatening player (plotted in black) is playing against a threat averse player (plotted in grey):

Conclusion

The main thing that needs to be highlighted before concluding is that this analysis has two weaknesses:

• The data: what comes out of mathematical models is only as good as what goes in. Scraping the wiki data is a cool thing to do (from a Python point of view) but I’m blindly grabbing guides that might have poor information/opinions in them. This is worth remembering. If someone where to come up with their own threat/performance measures then this work could just be used on that. Ultimately the data available here is better than no data.
• I am not taking in to account team dynamics. I’m just looking at perceived threats from one hero to another. There are mathematical approaches that could be used to find the best combination of teams and I might get to that in other post one day. Nonetheless this has been a fun application of game theory and still has value I believe.

So to conclude, basing things on the data available to me, I’d suggest that (when both players are acting in a risk averse way) the choice of heros for an isolated job like jungling and/or laneing is in fact reduced to a set from:

• Adagio
• Catherine
• Koshka
• Petal
• Glaive
• Fortress

If you and your opponent aim to be threatening, the choice is from:

• Glaive
• Krul
• Taka

Finally if you aim to be threatening, playing against a player aiming to be risk averse the choice is from:

• Glaive
• Krul
• Catherine
• Taka
• Koshka

and vice versa:

• Adagio
• Catherine
• Petal
• Glaive
• Fortress

(Interestingly for this last type of game there were in general just 1 equilibrium.)

Based on all of this, I would suggest (looking across all of that summary) that (disclaimer: based on the wiki threat data) the bestVainglory hero is Glaive. Again though, this does not take in to account any of the very important team dynamics. I plan to keep on being a protector with Ardan and just doing my best to stay alive…

Another point is that this shows that vainglory is perhaps not immediately balanced. A perfectly balanced game (like Rock Paper Scissor for example) has a Nash Equilibria that evenly plays all strategies:

sage:g=game_theory.normal_form_games.RPS()sage:g.obtain_nash()[[(1/3,1/3,1/3),(1/3,1/3,1/3)]]

Please do take a look at all the code/data at this repository.

This was a fun application of mathematical modelling, I also learnt how to scrape with BeautifulSoup but I mainly look forward to using this in my game theory class this year. I might even suggest we spend 25 minutes of one class having a game on the big screen assuming there are 5 players of Vainglory in my class.

Jim Simons

Jim Simons, after retiring from Renaissance Technologies with a cool 15 billion, has spent the last 10 years giving grants to people in the pure sciences. He's a true academic at heart [...] Anyways, he's very fond of academics and gives MacArthur-esque grants, especially to people who want to change the way mathematics is taught. Approach his fund. I'm 100% sure he'll give you a grant on the spot.

The National Science Foundation

Several million dollars per year

The purpose of this round table is to investigate what sorts of support would facilitate the development, deployment and maintenance of open-source software used for fundamental research in mathematics, statistics and theoretical physics. We hope that this group will consider what support is currently available, and whether there are projects that the Simons Foundation could undertake that would add significantly to the usefulness of computational tools for basic research. Modes of support that duplicate or marginally improve on support that is already available through the universities or the federal government will not be of interest to the foundation. Questions of software that is primarily educational in nature may be useful as a comparison, but are not of primary interest.  The scale of foundation support will depend upon what is needed and on the potential scientific benefit, but could be substantial, perhaps up to several million dollars per year.

Current modes of funding for research software in mathematics, statistics and physics differ very significantly. There may be correspondingly great differences in what the foundation might accomplish in these areas. We hope that the round table members will be able to help the foundation understand the current landscape  (what are the needs, what is available, whether it is useful, how it is supported) both in general and across the different disciplines, and will help us think creatively about new possibilities.

The Decision

We will not fund Sage

Dear William,

Before I joined the foundation, there was a meeting conducted by David Eisenbud to discuss possible projects in this area, including Sage.

After that meeting it was decided that the foundation would support Magma.

Please keep me in the loop regarding developments at Sage, but I regret that we will not fund Sage at this time.

Best regards, Yuri

Funding Open Source Mathematical Software in the United States

Why: Because Sage is Hobbling Along

Something that is Missing

Searching for a Funding Model

SageMath, Inc.

This Summer has seen 3 undergraduates carry out 8 week placements with me developing further game theoretic code in Sagemath:

Hannah Lorrimore (going in to her 2nd year) spent her placement working very hard to implement classes for extensive form games. These are mainly a graphical representation of games based on a tree like structure. Hannah not only developed the appropriate data structures but also worked hard to make sure the graphics looked good. You can see an example of the output below:

James Campbell (going in to an industrial placement year) picked up where he left off last Summer (James built the first parts of Game Theory code for Sagemath) and developed a test for degeneracy of games. This involves building a corresponding linear system for the game and testing a particular condition. James and I wrote a blog post about some of the theory here: http://vknight.org/unpeudemath/code/2015/06/25/on_testing_degeneracy_of_games/.

Rhys Ward (going in to his first year) has been working at the interface between extensive form games and normal form games. His main contribution (Rhys is still working as of the writing of this) has been to build code that converts an extensive form game to a normal form game. This requires carefully traversing the underlying tree and keeping track of the strategy space. Rhys has also built a catalog of normal form games and is now starting to work on the capability to remove dominated strategies from a normal form game.

Hannah, Rhys and James have also been working in conjunction with Tobenna Peter Igwe who is a PhD student at the University of Liverpool. Tobenna has been implementing a variety of game theoretic code as part of the Google Summer of Code project with me as his mentor.

Hannah, James, Tobenna and I visited Oxford University to spend two days working with Dr Dima Pasechnik and giving a talk. You can see a video of the talk here: https://www.youtube.com/watch?v=v4kKYr5I2io

All of this code will now be reviewed by the Sagemath community and will (just as James’s code last year) be eventually available to anyone who wants to study game theory.

Note: this blog post is based on a similar Cardiff University newsletter item.

Poor retention rate

Is it performance?

Is it the user interface?

Is it the open source software?

Is it support?

Why don't you use SageMathCloud?

Diagnose the problem

Justification

Guiding policies

Justification

• employees/engineers in various industries (from defense contractors, to finance, to health care to "data science").
• researchers in area of mathematics where Sage is currently not popular
• undergraduate students in STEM courses (science, tech, engineering, math)

Actions

• (a) Make access to Sage as easy as possible.
• (b) Encourage the creation of educational resources (books, tutorials, etc.) that make using Sage for particular courses as easy as possible.
• (c) Implement missing functionality in Sage that is needed in support of undergraduate teaching.

Justification

On Wednesday I was invited to participate in a Webinar entitled “Getting your first lecturship”. This was organised by Cardiff University’s graduate college (UGC). The format included an overview of recent findings from a survey conducted by the Association of Careers Advisory Services and then a discussion including Dr Sophie Coulombeau and Dr Claire Shaw.

You can see the recording below:

Here is the UGC page which includes a pdf with a variety of hopefully useful resources.

Sophie and Claire had some excellent advice and I would really recommend watching the video if you are at a stage of your academic career (PhD, postdoc…) and thinking of getting a lectureship in the United Kingdom (it’s probably useful in other countries also, but we concentrated on particularities of the UK).

Some of the particular points that stayed with me:

• Self care: it’s very easy to let academia do a lot of damage. This is not something I’m particularly good at myself but stress and mental health is something that you should always keep an eye on: at whatever stage of your career you are.
• Selling the whole narrative: at interview it’s important to find a way to think about what a particular post is looking for and how/why you fit that particular role.

What was also interesting was that we all seemed to agree that we were lucky. This was certainly the case with me, circumstances were just right and I was very lucky to have leadership that gave me a wealth of opportunities.

On a slightly related note, as I was writing this post, I thought about Tim Hopper’s great resource shouldigetaphd.com/. If you are thinking about doing a PhD at all, perhaps take a look at the awesome case stories there…

In a previous post I wrote about the podcasts I listen to. I really need to update that as things have changed but this post is not the update. In this post I’ll discuss some of my early thoughts as I get in to reddit.

My first real encounter of reddit was when u/I_feel_shy posted a link to my blogpost about Clash of clans. I create an account to be able to answer some questions on there but never really stayed put.

I think that one of the reasons for this was that I didn’t stumble on a mobile app I liked. This changed when @mkbhd posted a video mentioning that his app of choice was Relay for reddit.

So for about 2 months or so I’ve been using reddit regularly, and I have to admit that it’s become one of the first things I check whenever I get a chance. I think it’s the simplicity of it all that I like.

Here are the subreddits I subscribe to (please do let me know which ones I’m missing):

• r/android: I use an android phone and this seems to suggest neat apps, and let me know what’s coming up.
• r/AskAcademic: this has a variety of interesting discussions about Academia, with questions from students and faculty.
• r/askscience: a nice reddit with interesting questions that pop up, a neat one recently was “why can’t I weigh the earth by putting a scale upside down”.
• r/dataisbeautiful: cool data related stuff :)
• r/education: am still undecided as to whether or not I find this a valuable subreddit. I will wait and see…
• r/GAMETHEORY: not a very busy subbredit but everynow and then something interesting comes up.
• r/learnpython: I’ve only just joined this one. Hoping I might be able to help with some questions but also see some neat resources etc…
• r/math: one of the mathematics subreddits.
• r/mathematics: another one :)
• r/nottheonion: if you haven’t heard of the onion go take a look and then this subreddit will make a lot of sense…
• r/Python: I learn a lot from scrolling through this…
• r/rugbyunion: I like rugby.
• r/sagemath: this is the subreddit for Sagemath, it’s not terribly active but every now and then something cool pops up.
• r/science: a general subreddit about science. Interesting things usually pop up here.
• r/sysor: this is the subreddit for Operational Research (etc…). I’ve pied up and answered a question here but otherwise have learnt a few neat things that have been going on.
• r/vim: vim is my editor of choice and it’s nice to see things trickle through here. Today I read about the Goyo plugin which I’m actually using whilst writing this post, on there.

I’m pretty sure I’m missing out a bunch of interesting subreddits so please let me know in the comments :)

I’m also still trying to figure out if reddit is a social network or not. The main reason for this is that I’m not sure if it’s cool to post links to my own blog posts on there or not. I’ve done this one or twice but ams still trying to figure out the correct protocol. In the mean time I continue to read, vote and sometimes comment. It’s a nice place (I know reddit does not have this reputation but perhaps I’m just staying in the right places…).

Guest post by Chao Xu

In the summer, I have extended the SAGE code base for matroids for Google Summer of Code. This post shows a few example of it’s new capabilities.

Connectivity

Let $M$ be a matroid with groundset $E$ and rank function $r$. A partition of the groundset $\{E_1,E_2\}$ is a $m$-separation if $|E_1|,|E_2|\geq m$ and $r(E_1)+r(E_2)-r(E)\leq m-1$. $M$ is called $k$-connected if there is no $m$-separation for any $m k$. The Fano matroid is an example of $3$-connected matroid.

The Fano matroid is not $4$-connected. Using the certificate=True field, we can also output a certificate that verify its not-$4$-connectness. The certificate is a $m$-separation where $m 4$. Since we know Fano matroid is $3$-connected, we know the output should be a $3$-separation.

We also have a method for deciding $k$-connectivity, and returning a certificate.

There are 3 algorithms for $3$-connectivity. One can pass it as a string to the algorithm field of is_3connected.

1. "bridges": The $3$-connectivity algorithm Bixby and Cunningham. [BC79]
2. "intersection": the matroid intersection based algorithm
3. "shifting": the shifting algorithm. [Raj87]

The default algorithm is the bridges based algorithm.

The following is an example to compare the running time of each approach.

The new bridges based algorithm is much faster than the previous algorithm in SAGE.

For $4$-connectivity, we tried to use the shifting approach, which has an running time of $O(n^{4.5}\sqrt{\log n})$, where $n$ is the size of the groundset. The intuitive idea is fixing some elements and tries to grow a separator. In theory, the shifting algorithm should be fast if the graph is not $4$-connected, as we can be lucky and find a separator quickly. In practice, it is still slower than the optimized matroid intersection based algorithm, which have a worst case $O(n^5)$ running time. There might be two reasons: the matroid intersection actually avoids the worst case running time in practice, and the shifting algorithm is not well optimized.

Matroid intersection and union

There is a new implementation of matroid intersection algorithm based on Cunningham’s paper [Cun86]. For people who are familiar with blocking flow algorithms for maximum flows, this is the matroid version. The running time is $O(\sqrt{p}rn)$, where $p$ is the size of the maximum common independent set, $r$ is the rank, and $n$ is the size of the groundset. Here is an example of taking matroid intersection between two randomly generated linear matroids.

Using matroid intersection, we have preliminary support for matroid union and matroid sum. Both construction takes a list of matroids.

The matroid sum operation takes disjoint union of the groundsets. Hence the new ground set will have the first coordinate indicating which matroid it comes from, and second coordinate indicate the element in the matroid.

Here is an example of matroid union of two copies of uniform matroid $U(1,5)$ and $U(2,5)$. The output is isomorphic to $U(4,5)$.

One of the application of matroid union is matroid partitioning, which partitions the groundset of the matroid to minimum number of independent sets. Here is an example that partitions the edges of a graph to minimum number of forests.

Acknowledgements

I would like to thank my mentors Stefan van Zwam and Michael Welsh for helping me with the project. I also like to thank Rudi Pendavingh, who have made various valuable suggestions and implemented many optimizations himself.

References

[BC79] R.E Bixby, W.H Cunningham. Matroids, graphs and 3-connectivity, J.A Bondy, U.S.R Murty (Eds.), Graph Theory and Related Topics, Academic Press, New York (1979), pp. 91-103.

[Raj87] Rajan, A. (1987). Algorithmic applications of connectivity and related topics in matroid theory. Northwestern university.

[Cun86] William H Cunningham. 1986. Improved bounds for matroid partition and intersection algorithms. SIAM J. Comput. 15, 4 (November 1986), 948-957.

I’ve written quite a few blog posts about Markov chains (it occupies a central role in quite a lot of my research). In general I visualise 1 or 2 dimensional chains using Tikz (the LaTeX package) sometimes scripting the drawing of these using Python but in this post I’ll describe how to use the awesome networkx package to represent the chains.

For all of this we’re going to need the following three imports:

from__future__importdivision# Only for how I'm writing the transition matriximportnetworkxasnx# For the magicimportmatplotlib.pyplotasplt# For plotting

Let’s consider the Markov Chain I describe in this post about waiting times in a tandem queue. You can see an image of it (drawn in Tikz) below:

As is described in that post, we’re dealing with a two dimensional chain and without going in to the details, the states are given by:

states=[(0,0),(1,0),(2,0),(3,0),(4,0),(0,1),(1,1),(2,1),(3,1),(4,1),(0,2),(1,2),(2,2),(3,2),(4,2),(0,3),(1,3),(2,3),(3,3),(0,4),(1,4),(2,4)]

and the transition matrix \(Q\) by:

Q=[[-5,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[1/2,-6,5,0,0,1/2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,1,-7,5,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,1,-7,5,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,1,-2,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0],[1/5,0,0,0,0,-26/5,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,1/5,0,0,0,1/2,-31/5,5,0,0,1/2,0,0,0,0,0,0,0,0,0,0,0],[0,0,1/5,0,0,0,1,-36/5,5,0,0,1,0,0,0,0,0,0,0,0,0,0],[0,0,0,1/5,0,0,0,1,-36/5,5,0,0,1,0,0,0,0,0,0,0,0,0],[0,0,0,0,1/5,0,0,0,1,-11/5,0,0,0,1,0,0,0,0,0,0,0,0],[0,0,0,0,0,2/5,0,0,0,0,-27/5,5,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,2/5,0,0,0,1/2,-32/5,5,0,0,1/2,0,0,0,0,0,0],[0,0,0,0,0,0,0,2/5,0,0,0,1,-37/5,5,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,0,2/5,0,0,0,1,-37/5,5,0,0,1,0,0,0,0],[0,0,0,0,0,0,0,0,0,2/5,0,0,0,1,-12/5,0,0,0,1,0,0,0],[0,0,0,0,0,0,0,0,0,0,2/5,0,0,0,0,-27/5,5,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,2/5,0,0,0,1/2,-32/5,5,0,1/2,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,2/5,0,0,0,1/2,-32/5,5,0,1/2,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,2/5,0,0,0,1/2,-7/5,0,0,1/2],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2/5,0,0,0,-27/5,5,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2/5,0,0,0,-27/5,5],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2/5,0,0,0,-2/5]]

To build the networkx graph we will use our states as nodes and have edges labeled by the corresponding values of \(Q\) (ignoring edges that would correspond to a value of 0). The neat thing about networkx is that it allows you to have any Python instance as a node:

G=nx.MultiDiGraph()labels={}edge_labels={}fori,origin_stateinenumerate(states):forj,destination_stateinenumerate(states):rate=Q[i][j]ifrate>0:G.add_edge(origin_state,destination_state,weight=rate,label="{:.02f}".format(rate))edge_labels[(origin_state,destination_state)]=label="{:.02f}".format(rate)

Now we can draw the chain:

plt.figure(figsize=(14,7))node_size=200pos={state:list(state)forstateinstates}nx.draw_networkx_edges(G,pos,width=1.0,alpha=0.5)nx.draw_networkx_labels(G,pos,font_weight=2)nx.draw_networkx_edge_labels(G,pos,edge_labels)plt.axis('off');

You can see the result here:

As you can see in the networkx documentatin:

Yes, it is ugly but drawing proper arrows with Matplotlib this way is tricky.

So instead I’m going to write this to a .dot file:

nx.write_dot(G,'mc.dot')

Once we’ve done that we have a standard network file format, so we can use the command line to convert that to whatever format we want, here I’m creating the png file below:

$ neato -Tps -Goverlap=scale mc.dot -o mc.ps; convert mc.ps mc.png

The .dot file is a standard graph format but you can also just open up the .ps file in whatever you want and modify the image. Here it is in inkscape:

Even if the above is not as immediately esthetically pleasing as a nice Tikz diagram (but how could it be?) it’s a nice quick and easy way to visualise a Markov chain as you’re working on it.

Here is a JuPyTer notebook with all the above code.

Overview

Clay Mathematics Institute Lectures: 2005

Classical Fourier Transform

SIMUW

Reader feedback: "I dare you to find a typo!"

Designing the cover

Publishing with Cambridge University Press

What is was like for us working with CUP

The Future

Conclusions

1. Publishing a high quality book is a long and involved process.
2. Working with CUP has been frustrating at times; however, they have recruited a very strong team this year that addresses most issues.
3. I hope mathematicians will put more effort into making mathematics accessible to non-mathematicians.
4. Hopefully, this talk will give provide a more glimpse into the book writing process and encourage others (and also suggest things to think about when choosing a publisher and before signing a book contract!)

A common misconception about evolution is that “The fittest organisms in a population are those that are strongest, healthiest, fastest, and/or largest.” However, as that link indicates, survival of the fittest is implied at the genetic level: and implies that evolution favours genes that are most able to continue in the next generation for a given environment. In this post, I’m going to take a look at a high performing strategy from the Iterated Prisoner’s dilemma that was obtained through an evolutionary algorithm. I want to see how well it does in other environments.

Background

This is all based on the Python Axelrod package which makes iterated prisoner dilemma research straightforward and really is just taking a look at Martin Jones’s blog post which described the evolutionary analysis performed to get a strategy (EvolvedLookerUp) that is currently winning the overall tournament for the Axelrod library (with 108 strategies):

The strategy in question is designed to do exactly that and as you can see does it really well (with a substantial gap between it’s median score and the runner up: DoubleCrosser).

There are some things lacking in the analysis I’m going to present (which strategies I’m looking at, number of tournaments etc…) but hopefully the numerical analysis is still interesting. In essence I’m taking a look at the following question:

If a strategy is good in a big environment, how good is it in any given environment?

From an evolutionary point of view this is kind of akin to seeing how good a predator a shark would be in any random (potentially land based) environment…

 Generating the data

Thanks to the Axelrod, library it’s pretty straightforward to quickly experiment with a strategy (or group of strategies) in a random tournament:

importaxelrodasaxl# Import the axelrod librarydefrank(strategies,test_strategies,repetitions=10,processes=None):"""Return the rank of the test_strategy in a tournament with given    strategiess"""forsintest_strategies:strategies.append(s())nbr=len(test_strategies)tournament=axl.Tournament(strategies,repetitions=repetitions,processes=processes)results=tournament.play()returnresults.ranking[-nbr:],results.wins[-nbr:]

This runs a tournament and returns the rankings and wins for the input strategies. For example, let’s see how Cooperator and Defector do in a random tournament with 2 other strategies:

>>>importaxelrodasaxl>>>importrandom>>>random.seed(1)# A random seed>>>strategies=random.sample([s()forsinaxl.strategies],2)>>>strategies# Our 2 random strategies[TrickyDefector,Prober3]

We can then use the above function to see how Cooperator and Defector do:

>>>rank(strategies,[axl.Cooperator(),axl.Defector()])([3,2],[[0,0,0,0,0,0,0,0,0,0],[2,2,2,2,2,2,2,2,2,2]])

We see that cooperator ranks last (getting no wins), and defector just before last (getting 2 wins). This is confirmed by the actual tournament results:

The idea is to reproduce the above for a variety of tournament sizes, repeating random samples for each size and looking at the wins and ranks for the strategies we’re interested in.

This script generates our data:

importaxelrodasaxlimportcsvimportrandomimportcopymax_size=25# Max size of tournaments considered (maximum size of the sample)tournaments=20# Number of tournaments of each size to run (number of samples)repetitions=10# Number of repetitions of each tournament (for a given sample)test_strategies=[axl.EvolvedLookerUp,axl.TitForTat,axl.Cooperator,axl.Defector,axl.DoubleCrosser]strategies=[s()forsinaxl.strategiesifaxl.obey_axelrod(s)andsnotintest_strategies]defrank(strategies,test_strategies=test_strategies,repetitions=10,processes=None):"""Return the rank of the test_strategy in a tournament with given    strategiess"""forsintest_strategies:strategies.append(s())nbr=len(test_strategies)tournament=axl.Tournament(strategies,repetitions=repetitions,processes=processes)results=tournament.play()returnresults.ranking[-nbr:],results.wins[-nbr:]f=open('combined-data','w')csvwrtr=csv.writer(f)f_lookerup=open('data-lookerup.csv','w')csvwrtr_lookerup=csv.writer(f_lookerup)f_titfortat=open('data-titfortat.csv','w')csvwrtr_titfortat=csv.writer(f_titfortat)f_cooperator=open('data-cooperator.csv','w')csvwrtr_cooperator=csv.writer(f_cooperator)f_defector=open('data-defector.csv','w')csvwrtr_defector=csv.writer(f_defector)f_doublcrosser=open('data-doublecrosser.csv','w')csvwrtr_doublcrosser=csv.writer(f_doublcrosser)data=[]ind_data=[[],[],[],[],[]]forsizeinrange(1,max_size+1):row=[size]ind_row=[copy.copy(row)for_inrange(5)]forkinrange(tournaments):s=random.sample(strategies,size)strategy_labels=";".join([str(st)forstins])trnmt_s=copy.copy(s)results=rank(copy.copy(s),test_strategies=test_strategies,repetitions=repetitions)row.append([strategy_labels,results[0]]+results[1])fori,tsinenumerate(test_strategies):trnmt_s=copy.copy(s)results=rank(copy.copy(s),test_strategies=[ts],repetitions=repetitions)ind_row[i].append([strategy_labels,results[0]]+results[1])data.append(row)csvwrtr.writerow(row)csvwrtr_lookerup.writerow(ind_row[0])csvwrtr_titfortat.writerow(ind_row[1])csvwrtr_cooperator.writerow(ind_row[2])csvwrtr_defector.writerow(ind_row[3])csvwrtr_doublcrosser.writerow(ind_row[4])f.close()f_lookerup.close()f_titfortat.close()f_cooperator.close()f_defector.close()f_doublcrosser.close()

The above creates tournaments up to a size of 25 other strategies, with 20 random tournaments for each size, creating six data files:

• Data for tournaments with a random strategy sample and EvolvedLookerUp
• Data for tournaments with the random strategy sample and TitForTat
• Data for tournaments with the random strategy sample and Cooperator
• Data for tournaments with the random strategy sample and Defector
• Data for tournaments with the random strategy sample and DoubleCrosser
• Data for tournaments with the random strategy sample as well as the above strategies

Analysing the data

I then used this JuPyTer notebook to analyse the data.

Here is what we see for the EvolvedLookerUp strategy:

The line is fitted to the median rank and number of wins (recall for each number of strategies, 20 different sampled tournaments are considered) We see that (as expected) as the number of strategies increases both the median rank and wins increases, but what is of interest is the rate at which that increase happens.

Below is the fitted lines for all the considered strategies:

Here are the fits (and corresponding plots) for the ranks:

• EvolvedLookerUp: \(y=0.49x-0.10\) plot
• TitForTat: \(y=0.53-0.45\) plot
• Cooperator: \(y=0.42x+1.40\) plot
• Defector: \(y=0.75x-0.33\) plot
• DoubleCrosser: \(y=0.51x-0.47\) plot

Here are the fits (and corresponding plots) for the wins:

• EvolvedLookerUp: \(y=0.28x+0.06\) plot
• TitForTat: \(y=0.00x+0.00\) plot
• Cooperator: \(y=0.00x+0.00\) plot
• Defector: \(y=0.89x+0.14\) plot
• DoubleCrosser: \(y=0.85-0.10\) plot

It seems that the EvolvedLookerUp strategy does continue to do well (with a low coefficient of 0.49) in these random environments. However what’s interesting is that the simple Cooperator strategy also seems to do well (this might indicate that the random samples are creating ‘overly nice’ conditions).

All of the above keeps the 5 strategies considered separated from each, here is the analysis repeated when combining the strategies with the random sample:

Below is the fitted lines for all the considered strategies:

Here are the fits (and corresponding plots) for the ranks:

• EvolvedLookerUp: \(y=0.42x+2.05\) plot
• TitForTat: \(y=0.44+1.95\) plot
• Cooperator: \(y=0.64+0.00\) plot
• Defector: \(y=0.47x+1.87\) plot
• DoubleCrosser: \(y=0.63x+1.88\) plot

Here are the fits (and corresponding plots) for the wins:

• EvolvedLookerUp: \(y=0.28x+0.05\) plot
• TitForTat: \(y=0.00x+0.00\) plot
• Cooperator: \(y=0.00x+0.00\) plot
• Defector: \(y=0.89x+4.14\) plot
• DoubleCrosser: \(y=0.85+2.87\) plot

Conclusion

It looks like the EvolvedLookerUp strategy continues to perform well in environments that are not the ones it evolved in.

The Axelrod library makes this analysis possible as you can quickly create tournaments from a wide library of strategies. You could also specify the analysis further by considering strategies of a particular type. For example you could sample only from strategies that act deterministically (no random behaviour):

>>>strategies=[s()forsinaxl.strategiesifnots().classifier['stochastic']]

It would probably be worth gathering even more data to be able to make substantial claims about the performances as well as considering other test strategies but ultimately this gives some insight in to the performances of the strategies in other environments.

For fun

The latest release of the library (v0.0.21) includes the ability to draw sparklines that give a visual representation of the interactions between pairs of strategies. If you’re running python 3 you can include emoji so here goes the sparklines for the test strategies considered:

>>>fromitertoolsimportcombinations>>>test_strategies=[axl.EvolvedLookerUp,axl.TitForTat,axl.Cooperator,axl.Defector,axl.DoubleCrosser]>>>matchups=[(match[0](),match[1]())formatchincombinations(test_strategies,2)]>>>formatchupinmatchups:....match=axl.Match(matchup,10)...._=match.play()....print(matchup)....print(match.sparklines(c_symbol=' 😀 ',d_symbol=' 😡 '))...(EvolvedLookerUp,TitForTat)😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀(EvolvedLookerUp,Cooperator)😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀(EvolvedLookerUp,Defector)😀😀😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡(EvolvedLookerUp,DoubleCrosser)😀😀😡😡😀😀😀😀😀😀😀😡😡😡😡😡😡😡😡😡(TitForTat,Cooperator)😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀😀(TitForTat,Defector)😀😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡😡(TitForTat,DoubleCrosser)😀😀😡😡😡😡😡😡😡😡😀😡😡😡😡😡😡😡😡😡(Cooperator,Defector)😀😀😀😀😀😀😀😀😀😀😡😡😡😡😡😡😡😡😡😡(Cooperator,DoubleCrosser)😀😀😀😀😀😀😀😀😀😀😀😡😡😡😡😡😡😡😡😡(Defector,DoubleCrosser)😡😡😡😡😡😡😡😡😡😡😀😡😡😡😡😡😡😡😡😡

This blog post is a direct application of Cunningham’s Law: which is that “the best way to get the right answer on the Internet is not to ask a question, it’s to post the wrong answer”. With the other core developers of the Axelrod library we’re writing a paper and I wanted to see the evolution of a particular property of the library through the 2000+ commits (mainly to include a nice graph in the paper). This post will detail how I’ve cycled through all the commits and recorded the particular property I’m interested in. EDIT: thanks to Mario for the comments: see the edits in bold to see the what I didn’t quite get right.

The Axelrod library is a collaborative project that allows anyone to submit strategies for the iterated prisoner’s dilemma via pull request (read more about this here: axelrod.readthedocs.org/en/latest/). When the library was first put on github it had 6 strategies, it currently has 118. This figure can be obtained by simply running:

>>>importaxelrod>>>len(axelrod.strategies)118

The goal of this post is to obtain the plot below:

EDIT: here is the correct plot:

Here is how I’ve managed that:

1. Write a script that imports the library and throws the required data in to a file.
2. Write another script that goes through the commits and runs the previous script.

So first of all here’s the script that gets the number of strategies:

importaxelrodfromsysimportargvtry:iftype(len(axelrod.strategies))isint:printargv[1],len(axelrod.strategies),argv[2]except:pass

The (very loose) error handling is because any given commit might or might not be able to run at all (for a number of reasons). The command line arguments are so that my second script can pass info about the commits (date and hash).

Here is the script that walks the github repository:

fromgitimportRepo# This imports the necessary class from the gitPython packageimportosimportsubprocessimporttimepath_to_repo="~/src/Axelrod/"repo=Repo(path_to_repo)all_commits=[cforcinrepo.iter_commits()]# Get all the commitsgit=repo.git# This creates an object that I can just use basic git commands withgit.checkout('master')# Make sure I start at mastertime.sleep(10)# Need to give time for files writetry:os.remove('data')# Delete the data file if it already existsexceptOSError:passforcinsorted(all_commits,key=lambdax:x.committed_date):# Go through all commitsforrubbishin[".DS_Store","axelrod/.DS_Store","axelrod/tests/.DS_Store","axelrod/strategies/.DS_Store"]:# Having to delete some files that were not in gitignore at the time of the committry:os.remove(path_to_repo+rubbish)exceptOSError:passgit.checkout(c)# Checkout the committime.sleep(10)# Need to let files writef=open('data',"a")subprocess.call(['python2','number_of_strategies.py',str(c.committed_date),c.hexsha],stdout=f)# Call the other script and output to the `data` filef.close()git.checkout('master')# Go back to HEAD of master

Now, I am not actually sure if I need the 10 seconds of sleep in there but it seems to make things a little more reliable (this is where I’m hoping some knowledgeable kind soul will point out something isn’t quite right).

Here is an animated gif of the library as the script checks through the commits (I used a sleep of 0.1 second here, and cut if off at the beginning):

(You can find a video version of the above at the record.it site.)

The data set from above looks like this:

...
1424259748 6 5774fec6b3029b60c6b1bf4cb5d8bfb5323a1ad3
1424259799 6 35db17958a93e66cc09a7e7b865127b8d20acd85
1424261483 6 79c03291a1f0211925755962411d28c932150aaa
1424264425 7 f4be6bcbe9e122eb036a141f48f5acbf03b9290c
1424264540 7 6f28c9f8653e39b496c872351bce5a420e474c17
1424264950 7 456d9d25dbc44e29dde6b39455d10314824479bb
1424264958 7 0c01b14b5c3180d9e4016b09e532410cafd53992
1424265660 7 3eeec928cb7261af797044ac3bde1b26e11a7897
1424266926 7 cf506116005acd5a450894ca67eb0b670d5fd597
1424268080 8 87aa895089cdb105471280a0c374623ee7f6c9ba
1424268969 7 d0c36795fd6a69f9a1558b0b1e738d7633eb1b8e
1424270889 8 d487a97c9327235c4c334b23684583a116cc407a
1424272151 8 e9cd655661d3cef0a6df20cc509ae5ac2431f896
...

That’s all great and then the plot above can be drawn straightforwardly. The thing is: I’m not convinced it’s worked as I had hoped. Indeed: c7dc2d22ff2e300098cd9b29cd03080e01d64879 took place on the 18th of June and added 3 strategies but it’s not in the data set (or indeed in the plot).

Also, for some reason the data set gets these lines at some point (here be gremlins…) ?????:

...
<class 'axelrod.strategies.alternator.Alternator'>
<class 'axelrod.strategies.titfortat.AntiTitForTat'>
<class 'axelrod.strategies.titfortat.Bully'>
<class 'axelrod.strategies.cooperator.Cooperator'>
<class 'axelrod.strategies.cycler.CyclerCCCCCD'>
<class 'axelrod.strategies.cycler.CyclerCCCD'>
<class 'axelrod.strategies.cycler.CyclerCCD'>
<class 'axelrod.strategies.defector.Defector'>
<class 'axelrod.strategies.gobymajority.GoByMajority'>
<class 'axelrod.strategies.titfortat.SuspiciousTitForTat'>
<class 'axelrod.strategies.titfortat.TitForTat'>
<class 'axelrod.strategies.memoryone.WinStayLoseShift'>
...

What’s more confusing is that it’s not completely wrong because that does overall look ‘ok’ (correct number of strategies at the beginning, end and various commits are right there). So does anyone know why the above doesn’t work properly?

I’m really hoping this xkcd comic kicks in and someone tells me what’s wrong with what I’ve done:

EDIT: Big thanks to Mario Wenzel below in the comments for figuring out everythig that wasn’t quite right.

Here’s the script to count the strategies (writing to file instead of piping and also with correct error catching to deal with changes within the library):

fromsysimportargvimportcsvtry:importaxelrodstrategies=[]try:iftype(axelrod.strategies)islist:strategies+=axelrod.strategiesexcept(AttributeError,TypeError):passtry:iftype(axelrod.ordinary_strategies)islist:strategies+=axelrod.ordinary_strategiesexcept(AttributeError,TypeError):passtry:iftype(axelrod.basic_strategies)islist:strategies+=axelrod.basic_strategiesexcept(AttributeError,TypeError):passtry:iftype(axelrod.cheating_strategies)islist:strategies+=axelrod.cheating_strategiesexcept(AttributeError,TypeError):passcount=len(set(strategies))f=open('data','a')csvwrtr=csv.writer(f)csvwrtr.writerow([argv[1],count,argv[2]])f.close()except:pass

Here is the modified script to roll through the commits (basically the same as before but it calls the other script with the -B flag (to avoid importing compiled files) and also without the need to sleep:

fromgitimportRepoimportaxelrodimportosimportsubprocessimporttimeimportcsvpath_to_repo="~/src/Axelrod"repo=Repo(path_to_repo)all_commits=[cforcinrepo.iter_commits()]git=repo.gitnumber_of_strategies=[]dates=[]git.checkout('master')try:os.remove('data')exceptOSError:passforcinsorted(all_commits,key=lambdax:x.committed_date):forrubbishin[".DS_Store","axelrod/.DS_Store","axelrod/tests/.DS_Store","axelrod/strategies/.DS_Store"]:# Having to delete some files that were not in gitignore at the time of the committry:os.remove(path_to_repo+rubbish)exceptOSError:passgit.checkout(c)try:subprocess.call(['python2','-B','number_of_strategies.py',str(c.committed_date),c.hexsha])dates.append(c.committed_date)exceptImportError:passgit.checkout('master')

It looks like you should delete all pyc files from the repository in question and run the second script with the -B tag.

Thanks again Mario!

This post gives a game theoretic explanation as to why we exchange gifts. On twitter @alexip tweeted “‘Let’s agree not to give each other presents for Christmas’ is just another case of the prisoner’s dilemma #gametheory”. This post builds on that and investigates the premise fully in an evolutionary context investigating different values of how good it feels to give and receive a gift :)

To illustrate this consider the situation where Alex and Camille are approaching Christmas:

Alex: How about we don’t buy Christmas present for each other this year?

Camille: Sounds great.

Let us describe how this situation corresponds to a prisoner’s dilemma.

• If Alex and Camille cooperate and indeed keep their promise of not getting gifts than let us assume they both get a utility of \(R\) (reward).
• If Alex cooperates but Camille decides to defect and nonetheless give a gift then Alex will feel a bit bad and Camille will feel good, so Alex gets a utility of \(S\) (sucker) and Camille a utility of \(T\) (temptation).
• Vice versa if Camille cooperates but Alex decides to give a gift.
• If both Alex and Camille go against their promise then they both get a utility of \(P\) (punishment).

This looks something like:

If we assume that we feel better when we give gifts and will be keen to ‘cheat’ a promise of not giving then that corresponds to the following inequality of utilities:

In this case we see that if Camille chooses to cooperate then Alex’s best response is to play defect (as \(T>R\)):

If Camille is indeed going to not give a gift, then Alex should give a gift.

Also if Camille chooses to defect then Alex’s best response is to defect once again (as \(P>S\)):

If Camille is going to ‘break the promise’ then Alex should give a gift.

So no matter what happens: Alex should defect.

In game theory this is what is called a dominating strategy, and indeed this situation is referred to as a Prisoner’s Dilemma and is what Alex was referring to in his original tweet.

How does reputation effect gift giving?

So far all we are really modelling is a SINGLE exchange of gifts. If we were to exchange gifts every year we would perhaps learn to trust each other, so that when Camille says they are not going to give a gift Alex has reason to believe that they will indeed not do so.

This is called an iterated Prisoner’s dilemma and has been the subject of a great amount of academic work.

Let us consider two types of behaviour that Camille and Alex could choose to exhibit, they could be:

• Alternator: give gifts one year and not give gifts the next.
• TitForTat: do whatever the other does the previous year.

Let us assume that Alex and Camille will be faced with this situation for 10 years. I’m going to use the Python Axelrod library to illustrate things:

>>>importaxelrodasaxl>>>alex,camille=axl.Alternator(),axl.TitForTat()>>>match=axl.Match([alex,camille],10)>>>_=match.play()>>>print(match.sparklines(c_symbol='😀',d_symbol='🎁'))😀🎁😀🎁😀🎁😀🎁😀🎁😀😀🎁😀🎁😀🎁😀🎁😀

We see that Alex and Camille never actually exchange gifts the same year (the 😀 means that the particular player cooperates, the 🎁 that they don’t and give a gift).

Most of the ongoing Iterated Prisoner’s Dilemma research is directly due to a computer tournament run by Robert Axelrod in the 1980s. In that work Axelrod invited a variety of computer strategies to be submitted and they then played against each other. You can read more about that here: axelrod.readthedocs.org/en/latest/reference/description.html but the important thing is that there are a bunch of ‘behaviours’ that have been well studied and that we will look at here:

1. Cooperator: never give gifts
2. Defector: always give gifts
3. Alternator: give gifts one year and not give gifts the next.
4. TitForTat: do whatever the other does the previous year.
5. TwoTitForTat: will start by not giving a gift but if the other player gives a gift will give a gift the next two years.
6. Grudger: start by not giving gifts but if at any time someone else goes against the promise: give a gift no matter what.

What we will now do is see how much utility (how people feel about their gift giving behaviour) if we have a situation where 6 people exchange gifts for 50 years and each person acts according to one of the above behaviours.

For our utility we will use the following values of \(R, P, S, T\):

Here is how we can do this in python:

>>>family=[axl.Cooperator(),...axl.Defector(),...axl.Alternator(),...axl.TitForTat(),...axl.TwoTitsForTat(),...axl.Grudger()]>>>christmas=axl.Tournament(family,turns=50,repetitions=1)>>>results=christmas.play()>>>results.scores[[525],[562],[417],[622],[646],[646]]

We see that the people that do the best are the last two: TwoTitForTat and Grudger. These are people who are quick enough to react to people who won’t keep their promise but that do give hope to people who will!

 At a population level: evolution of gift giving

We can consider this in an evolutionary context where we see how the behaviour is allowed to evolve amongst a whole population of people. This particular type of game theoretic analysis is concerned not in micro interactions but long term macro stability of the system.

Here is how we can see this using Python:

>>>evo=axl.Ecosystem(results)>>>evo.reproduce(100)>>>plot=axl.Plot(results)>>>plot.stackplot(evo)

What we see is that over time, the population evolves to only Cooperator, TitForTat, Grudger and TwoTitsForTat, but of course in a population with only those strategies everyone is keeping their promise, cooperating and not giving gifts.

Let us see how this changes for different values of \(R, P, S, T\).

To check if not giving presents is evolutionary stable we just need to see what the last population numbers are for the Alternator and Defector. Here is a Python function to do this:

>>>defcheck_if_end_pop_cooperates(r=3,p=1,s=0,t=5,...digits=5,family=family,turns=10000):..."""Returns a boolean and the last population vector"""...game=axl.Game(r=r,p=p,s=s,t=t)...christmas=axl.Tournament(family,turns=50,repetitions=1,game=game)...results=christmas.play()...evo=axl.Ecosystem(results)...evo.reproduce(turns)...last_pop=[round(pop,digits)forpopinevo.population_sizes[-1]]...returnlast_pop[1]==last_pop[2]==0,last_pop

We see that for the default values of \(R, P, S, T\) we have:

>>>check_if_end_pop_cooperates(r=3,p=1,s=0,t=5)(True,[0.16576,0.0,0.0,0.26105,0.28659,0.28659])

As already seen we have that for these values we end up with everyone keeping to the promise. Let us increase the value of \(T\) by a factor of 100:

>>>check_if_end_pop_cooperates(r=3,p=1,s=0,t=500)(False,[0.0,1.0,0.0,0.0,0.0,0.0])

We here see, that if the utility of giving a gift when the receiver is not giving one in return is very large, the overall population will always give a gift:

 Seeing the effect of how good giving gifts makes us feel

The final piece of analysis I will carry out is a parameter sweep of the above:

• \(5\leq T \leq 100\)
• \(3\leq R < T\)
• \(1\leq P < R\)
• \(0\leq S < P\)

All of this data sweep is in this csv file. Here is the distribution of parameters for which everyone gives a gift (reneging on the promise):

Here is the distribution of parameters for which everyone keeps their promise and does not give gifts:

We see that people keep their promise if the \(T\) utility (the utility of being tempted to break the promise) is very high compared to all other utilities.

Carrying out a simple logistic regression we see the coefficients of each of the variables as follows:

• \(P\): 3.007720
• \(R\): -2.830106
• \(S\): 0.010675
• \(T\): -0.107508

The parameters that have a positive effect on keeping the promise is \(R\) and \(S\) which is the reward for the promise being kept and for not giving a gift but receiving one.

TLDR

Agreeing to not give gifts at Christmas can be an evolutionary stable strategy, but this is only in the specific case where the utility of ‘giving’ is less than the utility of ‘not giving’. Given that in practice this promise is almost always broken (that’s my personal experience anyway) this would suggest that people enjoy giving gifts a lot more than receiving them.

Merry christmas 🎄🎁⛄️.

• Jupyter notebook to produce graphics for this
• Python script to carry out parameter sweep
• The Axelrod library

• 3 at Google
• 1 at Facebook
• 1 at CCR

• Applying for many postdocs
• But just did summer internship at Microsoft Research with Kristin. (I’ve had four students do summer internships with Kristin)

• Have done a lot of Software development, maybe having little to do with math, e.g., “developing the Cython compiler”, “transition the entire Sage project to git”, etc.
• Did a thesis squarely in number theory, with significant theoretical content.
• Guilt (or guilty pleasure?) spending time on some programming tasks instead of doing what they are “supposed” to do as math grad students.

Me: academia and industry

• Math Ph.D. from Berkeley in 2000; many students of my advisor (Lenstra) went to work at CCR after graduating…
• Academia: I’m a tenured math professor (since 2005) – number theory.
• Industry: I founded a Delaware C Corp (SageMath, Inc.) one year ago to “commercialize Sage” due to VERY intense frustration trying to get grant funding for Sage development. Things have got so bad, with so many painful stupid missed opportunities over so many years, that I’ve given up on academia as a place to build Sage.

Advice for students from students

Robert Miller (Google)

Craig Citro (Google)

Rado Kirov (Google)

David Moulton (Google)

My advice for math professors

SageMathCloud course subscriptions

Getting started with SageMathCloud courses

I am writing this post just after two extraordinary weeks in Namibia. This is a quick personal reflection of what has been an awesome experience. As part of Cardiff University’s Phoenix Project, Martin Mugochi, Rob Wilson and I with Cardiff PhD students Geraint Palmer and Alex MacKay worked with the University of Namibia’s faculty of Mathematics to deliver a two week summer school.

The goal of this joint effort with the University of Namibia was to provide a positive experience of mathematics. As Rob said:

We want them to concentrate on what they can do rather than what they cannot do.

The first week involved inquiry based sessions on both mathematical topics (such as Algebra and Geometry) as well as wider skills (such as presenting and reading mathematics).

This side of the course mainly involved students working on through activities and presenting them to the class which lead to discussion (and in an IBL way ultimately confirmation/verification of the conclusions). This is the point at which we (I’m sure Rob, Alex and Geraint would agree) must say that the students were awesome. Eager to learn, open to the novel pedagogic ideas, a real pleasure to work with.

Here are some photos of the first week (the only local ones as I write this are from the group Alex and I took but things were pretty much the same in Rob and Geraint’s group):

The second week had students work in groups on a variety of projects such as:

• Mathematical paradoxes,
• Patterns in Pascal’s triangle,
• History of mathematics

From the intensity of the first week, this lead to a stark contrast in which students came to us for support. This lead to us not being in direct contact with all the students all the time.

The culmination of the whole school was a 2 hour closing ceremony in which students presented their posters. As we hadn’t seen all the groups we were slightly worried that this might fall flat on it’s face but we were very wrong and it was such a delight to see each and every group turn up to put their awesome poster on the wall.

Here are some of the posters:

Without any nudge on our part students starting walking around and learning from each other’s poster (I am still smiling about this now). This was followed by students giving 5 minute presentations, closing remarks from various UNAM officials, Martin Mugochi (head of the mathematics department) and ourselves.

One of my most pleasant memories (of which there are too many to mention) is what happened just after that though, we (students and us) came together to thank each other for our efforts and get photos:

This was such a great experience, it was fantastic to work and become good friends with Martin, get to know the students (seeing the benefits of active pedagogic methodologies) and spend two great weeks with Geraint, Alex and Rob:

This is just one of many Phoenix project projects and it’s great to be involved.

Now I need to put this laptop down, get a good night’s sleep and spend tomorrow working on final details for PyCon Namibia.