I've been using databases and doing web development for over 20 years, and I've never really
loved any database before and definitely didn't love any web development frameworks either. That all changed for me this summer...
SageMathCloud
SageMathCloud is a web application in which you collaboratively use Python, LaTeX, Markdown, Sage worksheets (sophisticated mathematics), task lists, R, Jupyter Notebooks, manage courses, write C programs, make chatrooms, and more. It is hosted on Google Compute Engine, but is also
entirely open source and there is a pre-made Virtual Machine that you can download. A
project in SMC is a Linux account, with resources constrained using cgroups and quotas. Many SMC users can
collaborate on the same project, and have equal privileges in that project. Interaction with all file types (including Jupyter notebooks, task lists and course managements) is synchronized in realtime, like Google docs. There is also a
global notifications feed that shows all editing activity on all files in all projects on which the user collaborates, which is a sort of highly technical version of Facebook's feed.
Rewrite motivation
I originally wrote the
SageMathCloud frontend using progressive-refinement jQuery (no third-party framework beyond that) and the Cassandra database. These were reasonable choices when I started. There are much better approaches now, which are critical to dramatically improving the user experience with SMC, and also growing the developer base. So far SMC has had no nontrivial outside contributions, probably due to the difficulty of understanding the code. In fact, I think nobody besides me has ever even
installed SMC, despite
these install notes.
We (me, Jon Lee, Nicholas Ruhland) are currently completely rewriting the entire frontend of SMC using React.js, Flux, and RethinkDB. We started this rewrite in June 2015, with Jon being supported by Google Summer of Code (2015), Nich being supported some by NSF grants from Randy Leveque and Rekha Thomas, and with me being unemployed.
Terrible funding situation
I'm living on credit cards -- I have no NSF grant support anymore, and SageMathCloud is still losing a lot of money every month, and I'm unhappy about this situation. It was either completely quit working on SMC and instead teach or consult a lot, or lose tens of thousands of dollars. I am doing the latter right now. I was very caught off guard, since this is my first summer ever to not have NSF support since I got my Ph.D. in 2000, and I didn't expect to have my grant proposals all denied (which happened in June). There is some modest Angel investment in SageMath, Inc., but I can't bring myself to burn through that money on salary, since it would run out quickly, and I don't want to have to shut down the site due to not being able to pay the hosting bill. I've failed to get any significant free hosting, due to already getting free hosting in the past, and SageMath, Inc. not being in any incubators. For example, we tried very hard to get hosting from Google, but they flatly refused for these two reasons (they gave $60K in hosting to UW/Sage project in 2012). I'm clearly having trouble transitioning from an academic to an industry funding model. But if there are enough paying customers by January 2016, things will turn around.
Jon, Nich, and I have been working on this rewrite for three months, and hope to finish it by the end of September, when Jon and Nich will become busy with classes again. However, it seems unlikely we'll be able to finish at the current rate. Fortunately, I don't start teaching fulltime again until January, and we put a lot of work into doing a release in mid-August that fully uses RethinkDB and partly uses React.js, so that we can finish the second stage of the rewrite iteratively, without any major technical surprises.
RethinkDB
Cassandra is an excellent database for many applications, but it is not the right database for SMC and I'm making no further use of Cassandra. SMC is a realtime application that does a lot more reading than writing to the database, and SMC greatly benefits from realtime push updates from the database. I've tried quite hard in the past to build an appropriate architecture for SMC on top of Cassandra, but it is the wrong tool for the job. RethinkDB scales up linearly (with sharding and replication), and has high availability and automatic failover as of version 2.1.2. See
https://github.com/rethinkdb/rethinkdb/issues/4678 for my painful path to ensuring RethinkDB actually works for me (the RethinkDB developers are incredibly helpful!).
React.js
I learned about React.js first from some "random podcast", then got more interested in it when Chris Swenson gave a demo at a Sage Days workshop in San Diego in May 2015. React (+Flux) is a web development framework that actually has solid
ideas behind it, backed by an implementation that has been optimized and tested by a highly nontrivial real world application: namely the Facebook website. Even if I were to have the idea of React, implementing in a way that is actually usable would be difficult. The key idea of React.js is that -- surprisingly -- it is possible to write efficient
client-side code that describes how to render the application purely as a function of its state.
React is
different than jQuery. With jQuery, you write lots of code explaining how to transform the user interface of your application from one complicated state (that you might never have anticipated happening) to another complicated state. When using React.js you don't write code about how your application's visible state changes -- instead you write code to answer the question: "given this state, what should the application look like". For me, it's a game changer. This is like what one does when writing video games; the innovation is that some people at Facebook figured out how to practically program this way in a client side web browser application, then tuned their implementation based on huge amounts of real world data (Facebook has users). Oh, and they open sourced the result and ran several conferences explaining React.
React.js reminds me of when Andrew Wiles proved Fermat's Last Theorem in the mid 1990s. Wiles (and Ken Ribet) had genuine new ideas, which dramatically reshaped the landscape of number theory. The best number theorists quickly realized this and adopted to the new world, pushing the envelope of Wiles work far beyond what I expected could happen. Other people pretended like Wiles didn't exist and continued studying Fibonnaci numbers. I browsed the web development section of Barnes and Noble last night and there were dozens of books on jQuery and
zero on React.js. I feel for anybody who tries to learn client-side web development by reading books at Barnes and Noble.
IPython/Jupyter and PhosphorJS
I recently met with Fernando Perez, who founded IPython/Jupyter. He seemed to tell me that currently 9 people are working fulltime on rewriting the Jupyter web notebook using the
PhosphorJS framework. I tried to understand PhosphorJS based on the github page, but couldn't, except to deduce that it is mostly the work of one person from Bloomberg/Continuum Analytics. Fernando told me that they chose PhosphorJS since it very fast, and that their main motivation is to (1) make Jupyter better use their huge high-resolution monitors on their new institute at Berkeley, and (2) make it easier for developers like me to integrate/extend Jupyter into their applications. I don't understand (2), because PhosphorJS is perhaps the least popular web framework I've ever heard of (is it a web framework -- I can't tell?). I pushed Fernando to explain why they made that design choice, but didn't really understand the answer, except that they had spent a lot of time investigating alternatives (like React first). I'm intimidated by their resources and concerned that I'm making the wrong choice; however, I just can't understand why they have made what seems to me to be the wrong choice. I hope to understand more at the joint
Sage/Jupyter Days 70 that we are organizing together in Berkeley, CA in November. (Edit: see
https://github.com/ipython/ipython/issues/8239 for a discussion of why IPython/Jupyter uses PhosphorJS.)
Tables and RethinkDB
Our rewrite of SMC is built on Tables, Flux and React.
Tables are client-side technology I wrote inspired by Facebook's GraphQL/Relay technology (and Meteor, Firebase, etc.); they synchronize data between clients and the backend database in realtime. Tables are defined by a
JSON schema file, which specifies the fields in the table, and explains what get and set queries are allowed. A table is a subset of a much larger table in the database, with the subset defined by conditions that are relative to the user making the query. For example, the projects table has one entry for each project that the user is a collaborator on.
Tables are automatically synchronized between the user and the database whenever the database changes, using
RethinkDB changefeeds.
RethinkDB's innovation is to build realtime updates -- triggered when the result of a query to the database changes -- directly into the database at the lowest level. Of course it is possible to build something that looks the same from the outside using either a message queue (say using RabbitMQ or ZeroMQ), or by watching the replication stream from the database and triggering actions based on that (like Meteor does using MongoDB). RethinkDB's approach seems better to me, putting the abstraction at the right level. That said, based on mailing list traffic, searches, etc., it seems that very, very few people get RethinkDB yet. Also, despite years of development, RethinkDB only became "production ready" a few months ago, and only got automatic failover a few weeks ago. That said, after ironing out some kinks, I'm now using it with heavy traffic in production and it works very well.
Flux
Once data is automatically synchronized between the database and web browsers in realtime, we can build everything else on top of this. Facebook also introduced an architecture pattern that they call
Flux, which works well with React. It's very different than MVC-style two-way binding frameworks, where objects are directly linked to UI elements, with an object changing causing the UI element to change and vice versa. In SMC each major part of the system has two objects associated to it: Actions and Stores. We think of them in terms of the classical CQRS pattern --
command
query
responsibility
segregation. Actions are commands -- they are Javascript "functions" that get stuff done, but they do not return values; instead, they impact the state of the store. The store has functions that allow one to query for the state of the store, but they do not change the state of the store. The store functions must only be functions of the internal state of the store and nothing else. They might cache their results and format their output to be very convenient for rendering. But that's it.
Actions usually cause the corresponding store (or stores) to change. When a store changes, it emit a change event, which causes any React components that depend on the store to be updated, which in many cases means they are re-rendered. There are optimizations one can introduce to reduce the amount of re-rendering, which if one isn't careful leads to subtle bugs; pretty much the only subtle React UI bugs one hits are caused by such optimizations. When the UI re-renders, the user sees their view of the world change. The user then clicks buttons, types, etc., which triggers actions, which in turn update stores (and tables, hence propogating changes to the ultimate source of truth, which is the RethinkDB database). As stores update, the UI again updates, etc.
Status
So far, we have completely (re-)written the project listing, file manager, help/status page, new file page, project log, file finder, project settings, course management system, account settings, billing, project upgrade system, and file use notifications using React, Flux, and Tables, and the result works well. Bugs are much easier to fix, and it is easy (possible?) to understand the state of the system, since it is defined by the state of the database and the corresponding client-side stores. We've completely rethought everything about the UI in doing the rewrite of the above components, and it has taken several months. Also, as mentioned above, I completely rewrote most of the backend to use RethinkDB instead of Cassandra. There were also the weeks of misery for me after we made the switch over. Even after weeks of thinking/testing/wondering "what could go wrong?", we found out all kinds of surprising little things within hours of pushing everything into production, which took more than a week of sleep deprived days to sort out.
What's left? We have to rewrite the file editor tabs system, the project tabs system, and all the applications (except course management): editing text files using Codemirror, task lists (which are suprisingly complicated!), color xterm terminals, Jupyter notebooks (which will still use an iframe for the notebook itself), Sage worksheets (with complicated html output embedded in codemirror), compressed file de-archiver, the LaTeX editor, the wiki and markdown editors, and file chat. We hope to find a clean way to abstract away the various SMC applications as plugins, so that other people can easily write their own applications/plugins that will run inside of SMC. There will be a rich collection of example plugins to build on, namely the ones listed above, which are all driven by critical-to-us real world applications.
Discussion about this blog post on Hacker News.


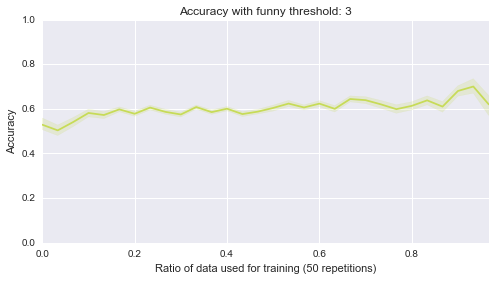
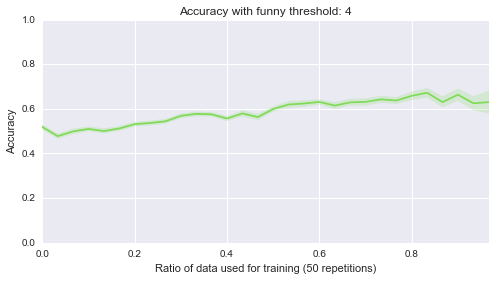
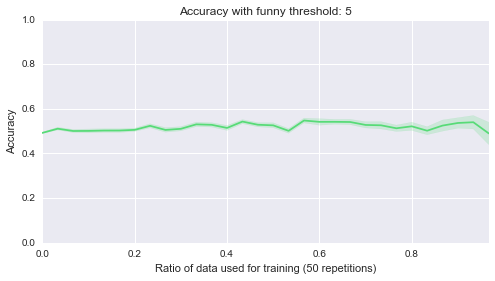
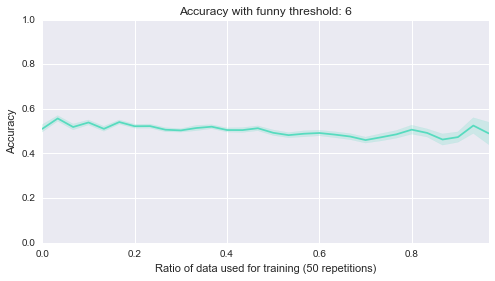


 The version that can be found on trac is only missing some doctests and a bit of documentation. Asymptotic expressions are the central objects within this project, and essentially they are sums of several asymptotic terms. In the background, we use a special data structure (“mutable posets“,
The version that can be found on trac is only missing some doctests and a bit of documentation. Asymptotic expressions are the central objects within this project, and essentially they are sums of several asymptotic terms. In the background, we use a special data structure (“mutable posets“,